Rechercher un outil (en entrant un mot clé):
Calculer la probabilité d'une Loi Normale
La variable aléatoire X suit la Loi Normale de paramètres µ et σ si sa loi de densité est donnée par la fonction suivante :
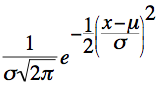
Propriétés :
Soit X une variable aléatoire suivant la loi normale de paramètres µ et σ.
- Son espérance est : E (X) = µ
- Sa variance est : V (X) = σ2
- Son écart-type est : σ (X) = σ
L'outil calcule les valeurs de P( X ≤ a ) et P( a ≤ X ≤ b ).
Loi Normale N(0,1) centrée réduite
P(−1 ≤ X ≤ 1) = 0.683 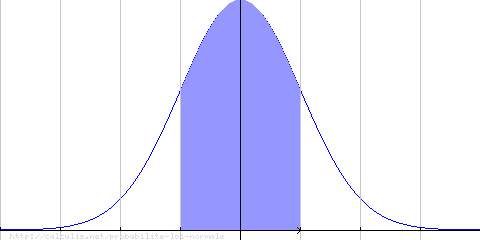
P(−2 ≤ X ≤ 2) = 0.954 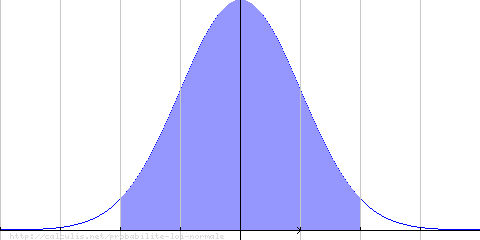
P(−3 ≤ X ≤ 3) = 0.997 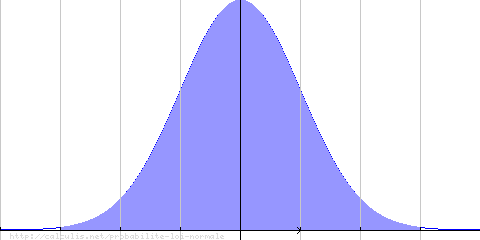
On a aussi :
P(−1.96 ≤ X ≤ 1.96) = 0, 95
P(−2.58 ≤ X ≤ 2.58) = 0, 99
Loi Normale N(µ,σ)
Exemple avec N(2,3):
P(µ − σ ≤ X ≤ µ + σ) = 0.68 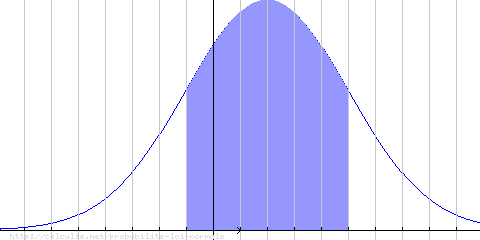
P(µ − 2σ ≤ X ≤ µ + 2σ) = 0.95 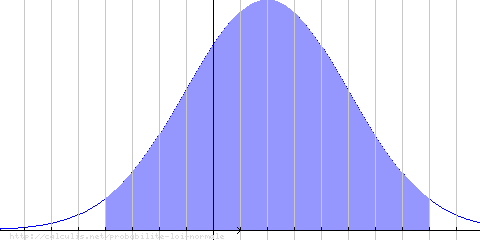
on a aussi :
P(µ − 3σ ≤ X ≤ µ + 3σ) = 0.997

