Rechercher un outil (en entrant un mot clé):
Calculer les produits en croix ou utilier la règle de trois
Dans un tableau de proportionnalité qui contient quatre valeurs, les produits des valeurs en "diagonales" sont égaux. On les appelle les produits en croix.
En utilisant cette règle des produits en croix, nous pouvons déduire la quatrième valeur à partir de trois valeurs déjà connues, afin de maintenir la proportionnalité du tableau. Cette quatrième valeur est souvent appelée "la quatrième proportionnelle". Elle est unique, car elle est la seule valeur qui rende le tableau proportionnel.
Cette méthode de calcul est couramment désignée sous le nom de "règle de trois". Elle est extrêmement utile pour résoudre des problèmes de proportionnalité dans divers domaines, tels que les finances, les sciences, ou les calculs commerciaux.
Soit un tableau (qui est proportionel) à 4 valeurs a, b, c et d :
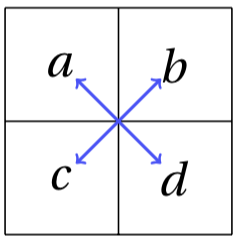
Alors les produits suivants sont égaux :
`a × d = b × c`.
Nous pouvons ainsi déterminer une des 4 valeurs, par exemple "d" avec l'égalité suivante :
`d = (b × c) ÷ a = {b × c} / a`.
Pour avoir une idée plus précise, prenez le temps de lire les exemples ci-dessous. L'outil peut vérifier si 4 valeurs sont proportionnelles. Pour cela, il suffit de renseigner les 4 champs.
Exemples d'utilisation des produits en croix
Parmi les nombreuses règles des Mathématiques, la règle de trois est une des plus utilisées dans la vie courante.
Exemple 1 : consommation moyenne de carburant
Quelle est le consommation moyenne en L/100km
Un véhicule a consommé 47.03 litres d'essence en parcourant 658 km. Quelle est la consommation moyenne en L aux 100 km de ce véhicule ?
On peut toujours présenté un problème de proportionnalité sous la forme d'un tableau :
| Litre | 47.03 | `x` |
| km | 658 | 100 |
Les produits en croix égaux sont les suivants : `47.03 × 100 = 658 × x`
Alors `x = {47.03 × 100} / 658 \approx 7,15` L/100km
Votre véhicule consomme 7,15 litres aux 100 km.
Exemple 2 : quantité de peinture
Quelle est la quantité de peinture nécessaire ?
Pour repeindre une salle, vous choisissez de la peinture avec les indications suivantes sur la notice technique : 2,5 litres de peinture permettent de couvrir 7 m². La peinture est vendue en pots de 2,5 L, en tines de 10 et 25 L. Plus la contenance est grande, plus le prix au litre est avantageux. Mais avez-vous réellement besoin de 25 L ?
Après calcul la superficie des murs de la salle représentent 85m2. Quelle sera la quantité de peinture nécessaire ?
Il faut 2,5 L pour 7 m2. Combien faut-il de Litres pour 84 m2 ?
On présente le problème sous la forme d'un tableau (comme dans l'outil de cette page).
| Litre | 2,5 | `x` |
| m2 | 7 | 84 |
Nous obtenons `x = {2,5 × 84} / 7 = 30 L`. Finalement, la tine de 25 L n'est pas suffisante.
Exemple 3 : des notes qui ne sont pas sur 20
Comment transformer une note sur 15, 25, 30 ou sur 77 en une note sur 20 ?
C'est un simple problème de proportionnalité. Vous avez obtenu 18 sur 30. Trouver l'équivalent de cette note sur 20 revient à chercher la valeur `x` telle que : " `x` vingtième soit égal à 18 trentième " .
C'est-à-dire on cherche `x` afin que `18 / 30 = x / 20`
De fait on a les égalités des produits en croix : `18 × 20 = x × 30`
Et ainsi `x = {18 × 20} / 30 = 12`.
Vous pouvez aussi raisonner dans ce sens "diviser par 30", ce qui vous permet de trouver combien vous avez eu sur 1 (c'est ce que l'on appelle le passage par l'unité), et ensuite multiplier par 20.
Les notes des dictées de primaire sont souvent données sur un nombre de difficultés, par exemple sur 77. Nous avons tellement l'habitude de l'échelle de valeur sur 20 qu'il nous est difficile d'apprécier une note sur 77.
Avoir 68 sur 77 correspond à quelle note sur 20 ? Il suffit de faire 68 divisé par 77 et ensuite de multiplier par 20 pour trouver le résultat : 68 ÷ 77 × 20 ≈ 17,662.
66 sur 77 correspond à la note 17,66 sur 20.
Commentaires
Bonjour, le résultat que vous donnez pour la consommation au 100 km est évidemment juste mais pour une personne qui ne maitrise pas la règle votre exemple n'est pas clair. Dans "47.03×100÷658" pouquoi mutiplier la consommation par 100 ? Au début la démarche est la suivante si je dépense 47.03 litres pour 658 km je cherche combien je dépense pour 1km et je multiplie par 100 afin d'obtenir la moyenne au 100 km, cela se traduit par "47.03÷658×100" ce qui me semble beaucoup plus clair pour le néophite .C'est ainsi que l'on m'a appris et j'ai tout de suite compris il en va de même pour le second exemple connaissant la surface couverte par 2,5 L de peinture. Il est logique de chercher combien de fois il y a 7 m2 dans 84 et ensuite on multiplie par 2,5 : 84÷7×2,5.
J'ai entendu dire que l'on ne voulait plus apprendre la règle de trois aux enfants car c'était trop compliquée ! Mais peut-être que la difficulté vient du fait que dans une équation on doit faire les multiplications avant les division (il me semble). Si je veux poser une règle de trois comme une équation , je devrais peut-être écrire `(47.03 / 658 ) × 100` = .
En "calcul ", comme on me l'a enseigné, on ne connait que 4 opérations et la règle de trois n'est qu'une contraction d'une division suivit d'une multiplication. C'est donc, logiquement, le résultat de la division qui doit être multiplié par 100. Une fois la règle de trois posée on peut, pour la simplification du calcul, faire la multiplication par 100 et ensuite la division...
`{47.03 × 100} / 658`
Félicitation pour votre site qui aide pas mal de gens excusez-moi de ne pas être tout à fait en accord avec vous j'ai 66 ans , il y a des lustre notre instituteur, nous avez appris cela bien avant les réformes.
Le 11-09-2013 Jean Louis M.
Réponse : Effectivement votre raisonnement est tout à fait logique. La quantité `{47.03}/658` représente bien quelque chose (le nombre de litres consommés pour 1 km), alors que dans ma présentation, la première opération `47.03×100` ne représente rien de tangible. J'espère que des internautes y trouveront une explication supplémentaire. De mon coté, je me suis attaché à faire comprendre que les produits en croix étaient égaux. 47.03×100 = 658×"la valeur inconnue", d'où l'apparition des opérations dans cet ordre :
"la valeur inconnue" = `{47.03×100}/658`.

