Rechercher un sujet parmi les questions (en entrant un mot clé):
Comment calculer l'apothème d'une pyramide
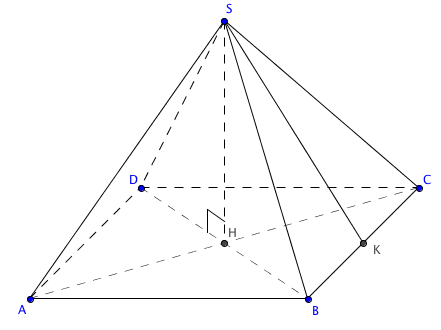
Considérons une pyramide réguliere à base carrée dont les cotés c mesurent 8 cm et dont la hauteur h mesure 10 cm. Comment calculer la mesure de l'apothème d et la mesure d'une arête a ?
Nous poursuivrons par le développement de la surface latérale de la pyramide, afin d'en calculer son aire.
Publié le 14/02/2013 à 16:20:13 - Auteur : Webmaster
REPONSES :
Une pyramide est réguliére lorsque sa base est un polygone régulier et que le pied de la hauteur coïncide avec le centre de la base. Dans la figure représente ci-dessus la pyramide est une pyramide régulière à basse carrée.
Dans une pyramide régulière les arêtes sont toutes égales et les faces latérales sont des triangles isocèles égaux. La hauteur SK du triangle SBC est appelée l'apothème de la pyramide.
Remarque : le triangle SBC étant isocèle, la hauteur SK est aussi la médiane et la médiatrice du segment [BC].
Dans le triangle SHK, on a :
SH = 10 cm et HK = 8÷2 = 4
Comme le triangle SHK est rectangle H, nous pouvons utiliser la propriété de Pythagore :
SK² = SH² + HK²
SK² = 10² + 4² = 116
d'où
SK = √116 = 2√29 ≈ 10,77 cm.
Dans le triangle SHA rectangle en H, nous utilisons aussi l'égalité de Pythagore :
SA² = SH² + HA²
SH = 10 cm
AC est la diagonale d'un carré de coté 8 cm donc AC = 8√2 cm d'où HA = 4√2 cm.
alors SA² = 10² + (4√2)² = 100 + 16×2 = 132 et de là SA = √132 = 2√33 ≈ 11,49 cm.
Conclusion : l'apothème est égal à 10,77 cm et une arête est égale à 11,49 cm.
Réponse publiée le 14/02/2013 à 19:01:44 - Auteur : Webmateur
On peut ajouter le calcul de la surface latérale de la pyramide. Cette surface est composée de 4 triangles isocèles dont on connait la base c (le coté de la base de la pyramide) et une hauteur a (l'apothème de la pyramide).
La surface latérale de la pyramide est donc égale à : 4×(c×a/2) = 4c.a/2 = p.a/2 où p est le périmètre de la base.
L'aire latérale d'une pyramide régulière est égale au demi-produit du périmètre de la base par l'apothème.
Dans notre exemple : S = 4×8×10,77÷2 = 16×10,77 = 172,32 cm².
Réponse publiée le 14/02/2013 à 20:29:27 - Auteur : Webmaster
Nous pouvons terminer par son volume V = c × h ÷ 3 = 8² × 10 ÷ 3 = 213,33 cm³.
Réponse publiée le 14/02/2013 à 20:33:03 - Auteur : Webmaster
Merci beaucoup, très utile...
Réponse publiée le 14/12/2014 à 10:46:54 - Auteur : webloser
Merci bcp!!!
Réponse publiée le 02/11/2015 à 17:06:26 - Auteur :
Merci beaucoup !!! J'ai fait ce calcul pour trouver l'aire totale de la pyramide du Louvre et cela m'a beaucoup aidé.
Réponse publiée le 01/11/2019 à 14:58:37 - Auteur : Anonyme
Bonjour, pourquoi divise t on l'a hauteur de l'apothème par 2 pour calculer l'aire latérale d'une pyramide ?
Réponse publiée le 24/04/2020 à 11:21:48 - Auteur : Alex Dupont
Bonjour, l'apothème joue de le rôle de hauteur pour chaque face et l'on reprend la formule d'un triangle : base × hauteur ÷ 2 .
Réponse publiée le 30/04/2020 à 16:56:45 - Auteur : Le webmaster

