Rechercher un outil (en entrant un mot clé):
Définition d'un cylindre
Un cylindre est une surface ou un solide géométrique composé de :
Qu'est-ce qu'un cylindre ? Définition et calcul de volume
En géométrie, un cylindre est une forme tridimensionnelle composée de :
- Deux bases circulaires identiques et parallèles (disques)
- Une surface latérale courbe reliant ces deux bases
Calcul du volume d'un cylindre droit
Pour calculer le volume d'un cylindre droit (le type le plus courant, comme une cannette ou un tube) :
- L'axe est perpendiculaire aux bases
- La hauteur (H) correspond à la distance entre les deux bases
- Le rayon (R) est la distance du centre à l'extérieur du disque de base
La formule du volume du cylindre est : V = π × R² × H
Où π ≈ 3,14, R est le rayon et H la hauteur
Exemple concret : Pour calculer le volume en litres d'un réservoir cylindrique de 1m de rayon et 2m de hauteur :
V = 3,14 × (1)² × 2 = 6,28 m³ soit 6280 litres
Calculer le volume d'un cylindre :
* si vous choisissez une unité pour les longueurs, l'outil calculera le volume du cylindre dans cette unité au cube et en litre.
Caractéristiques principales :
- Rayon (R) : Le rayon des disques qui forment les bases.
- Hauteur (H) : La distance perpendiculaire entre les deux bases.
Illustration :
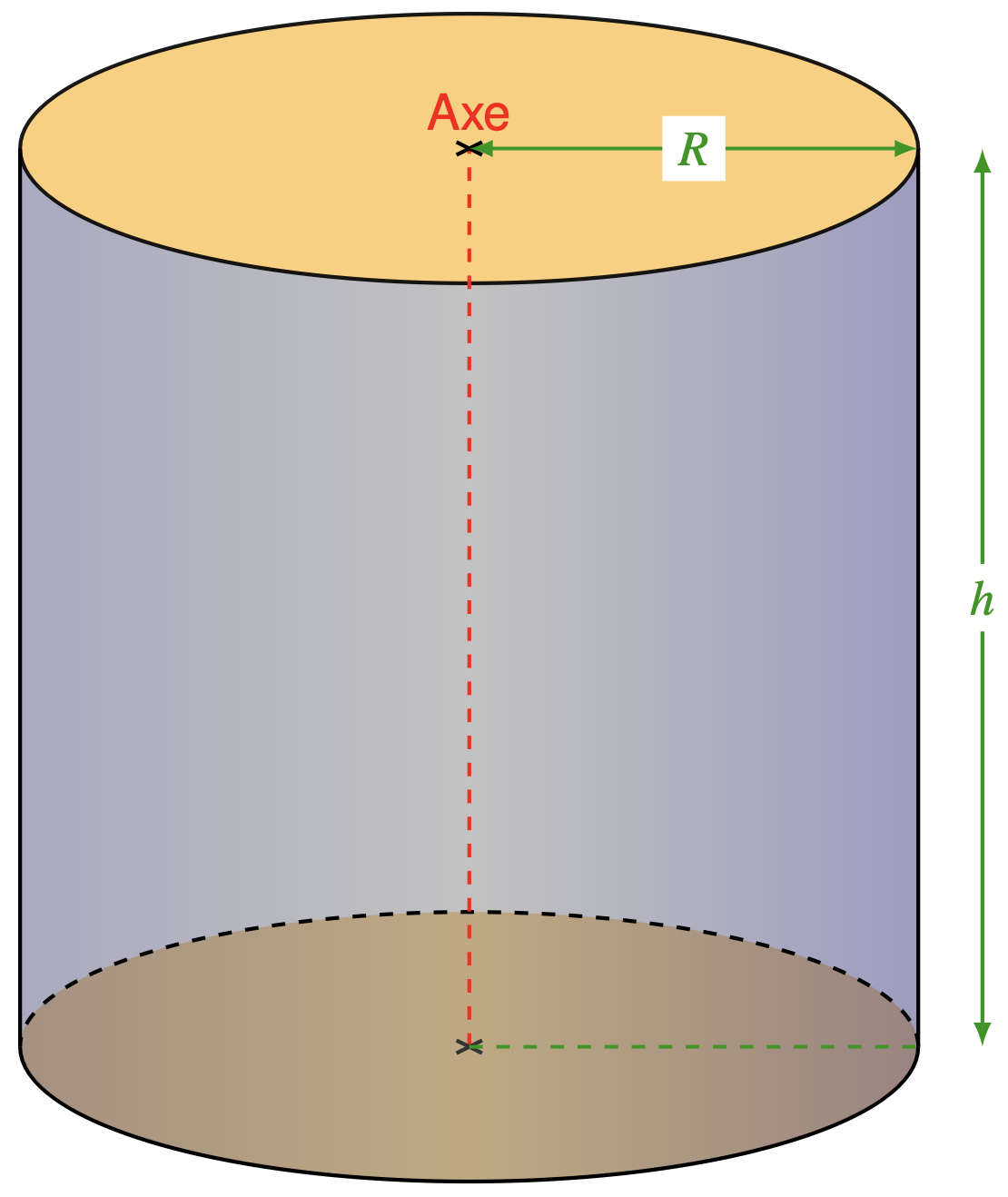
La formule du volume d'un cylindre
Le calcul du volume d'un cylindre repose sur une formule simple, basée sur :
- La hauteur (h) du cylindre.
- Le rayon (R) de la base circulaire.
Le volume (V) d'un cylindre est égal à l'aire de sa base (Aire_base) multipliée par sa hauteur (h). La base du cylindre étant un disque, son aire se calcule ainsi :
Aire_base = π × R²
La formule complète pour le volume devient :
Volume = Aire_base × Hauteur = (π × R²) × h
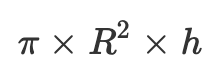
π (pi) est une constante mathématique, environ égale à 3,14159, utilisée dans les calculs liés aux cercles et cylindres.
Exemple : calculer le volume d'un cylindre en litre
Considérons un cylindre de diamètre 14 cm et de hauteur 10 cm :
- Formule : V = π × R² × h
- Calcul : V = π × 7² × 10 = π × 49 × 10
- Approximation : V ≈ 3,14159 × 490 = 1538,6 cm³
Le volume est donc 1538,6 cm³. Converti en litres :
- 1 litre = 1000 cm³
- 1538,6 cm³ = 1,5386 litre ≈ 1,5 litre.
Exemple : volume d'un récupérateur d'eau
Un récupérateur d'eau cylindrique a pour dimensions :
- Hauteur : 110 cm
- Diamètre : 100 cm
Rayon de la base : 50 cm
Calcul : V = π × R² × h
V = π × 50² × 110 ≈ 3,14159 × 2500 × 110 ≈ 863937,98 cm³ ≈ 863,94 litres.
Exemple : volume de fuel dans une cuve cylindrique
Une cuve cylindrique, avec :
- Diamètre : 130 cm
- Hauteur du fuel : 80 cm
Rayon : 65 cm
Calcul : V = π × R² × h
V = π × 65² × 80 ≈ 3,14159 × 4225 × 80 ≈ 1 061 858,32 cm³ ≈ 1 061,9 litres.
Il reste donc environ 1 061 litres de fuel dans la cuve.
Pour une cuve horizontale en forme de citerne, utilisez cet outil.
Propriétés d'un cylindre :
- Un cylindre de révolution est un solide droit avec des bases circulaires identiques.
- Les bases ont une aire égale à : π × R².
- L'axe passant par les centres des bases est perpendiculaire aux deux disques.

