Calculis

Le volume d'une pyramide régulière tronquée

Le volume d'une pyramide régulière tronquée, dont les surfaces de la grande et petite bases sont B et b et de hauteur h, est égal à :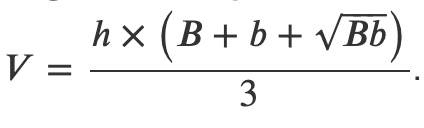

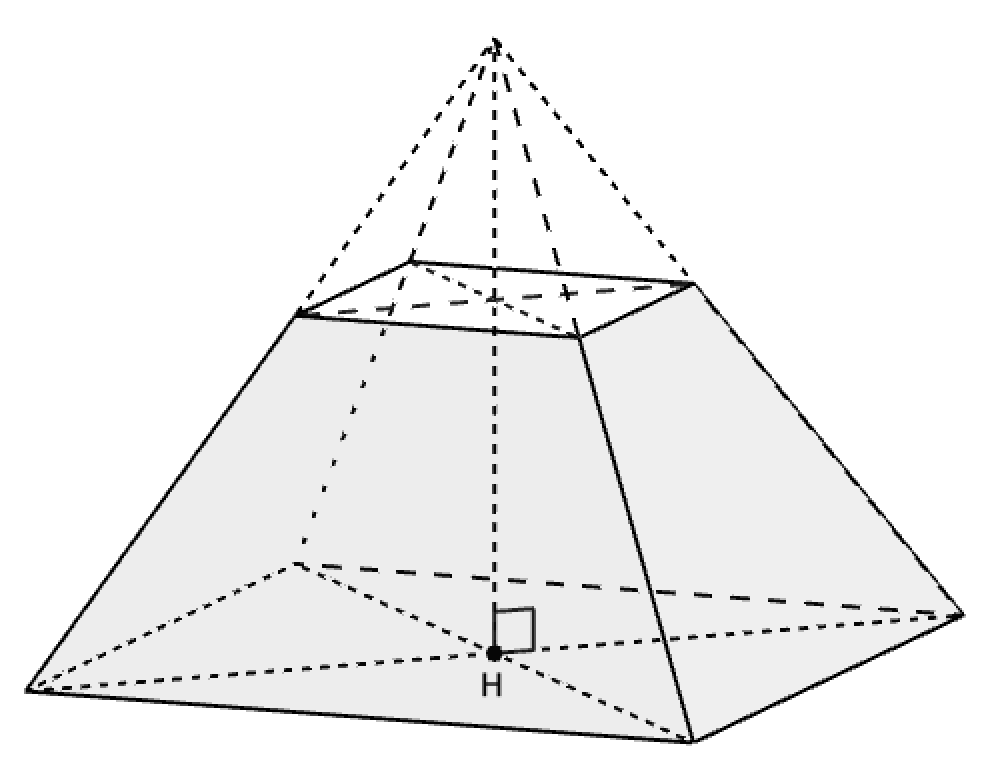
La hauteur h est la distance qui sépare les deux bases de la pyramide tronquée.

* Entrer les valeurs dans des unités cohérentes si les aires des surfaces des bases sont en m² , la hauteur doit être en m.

Remarque : la formule reste valable du moment que la grande base et la petite base de la pyramide tronquée sont semblables (de même forme, mais pas de la même taille) et que les plans définis par les bases sont parallèles.

Exemple numérique du calcul du volume d'une pyramide tronquée

Une bougie a la forme d'une pyramide régulière tronquée d'une hauteur de 7 cm. Le côté de la grande base carrée mesure 10 cm et le côté de la petite base mesure 5 cm.

Les surfaces des bases B et b sont égales à :

B = 10 × 10 = 100 cm²

b = 5 × 5 = 25 cm²,

alors le volume de cire est égal à :

V = 7 × (100 + 25 + √(100 × 25)) ÷ 3 = 408.33 cm³.

Exemples supplémentaires :

Exemple 1 : Une pyramide tronquée a une hauteur de 10 cm. Le côté de la grande base carrée mesure 12 cm et celui de la petite base 6 cm. Les surfaces des bases sont :

B = 12 × 12 = 144 cm²

b = 6 × 6 = 36 cm²

Le volume est :

V = 10 × (144 + 36 + √(144 × 36)) ÷ 3 = 10 × (144 + 36 + 72) ÷ 3 = 10 × 252 ÷ 3 = 840 cm³.

Exemple 2 : Une pyramide tronquée a une hauteur de 15 cm. Le côté de la grande base rectangulaire mesure 8 cm × 6 cm, et celui de la petite base mesure 4 cm × 3 cm. Les surfaces des bases sont :

B = 8 × 6 = 48 cm²

b = 4 × 3 = 12 cm²

Le volume est :

V = 15 × (48 + 12 + √(48 × 12)) ÷ 3 = 15 × (48 + 12 + 24) ÷ 3 = 15 × 84 ÷ 3 = 420 cm³.

Exemple 3 : Une pyramide tronquée avec une hauteur de 5 cm, une grande base circulaire de rayon 7 cm, et une petite base circulaire de rayon 3 cm. Les surfaces des bases sont :

B = π × 7² = 49π cm²

b = π × 3² = 9π cm²

Le volume est :

V = 5 × (49π + 9π + √(49π × 9π)) ÷ 3 ≈ 5 × (58π + 21π) ÷ 3 ≈ 5 × 79π ÷ 3 ≈ 414.69 cm³.