Rechercher un outil (en entrant un mot clé):
Calcul du volume d'un cône tronqué
Un cône tronqué est une portion d’un cône droit obtenue en coupant le cône par un plan parallèle à sa base. Il possède :
- Deux bases circulaires de rayons différents (R pour la grande base et r pour la petite base).
- Une hauteur (h) : distance perpendiculaire entre les deux bases.
Formule du volume :
Le volume d’un cône tronqué est donné par la formule :
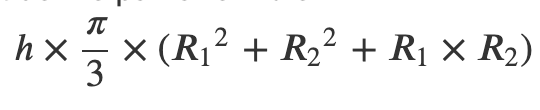
ou sous une forme équivalente :
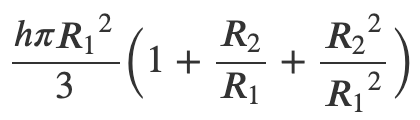
Dans cette formule :
- h : Hauteur du cône tronqué.
- R : Rayon de la grande base.
- r : Rayon de la petite base.
- π (pi) : Constante mathématique, environ égale à 3,14159.
Remarque :
Notre outil intègre cette formule pour permettre un calcul rapide et précis du volume d’un cône tronqué en fonction de sa hauteur et des rayons de ses bases.
Exemple de calcul :
Calculons le volume d'un cône tronqué avec :
- R = 10 cm (grande base).
- r = 5 cm (petite base).
- h = 12 cm (hauteur).
Étape 1 : Appliquer la formule
Volume = \[(1/3) × π × h × (R² + R × r + r²)\]
Volume = \[(1/3) × π × 12 × (10² + 10 × 5 + 5²)\]
Volume = \[(1/3) × π × 12 × (100 + 50 + 25)\]
Volume = \[(1/3) × π × 12 × 175\]
Étape 2 : Calcul
Volume = \[(1/3) × π × 2100\]
Volume ≈ \[3,14159 × 700 = 2199,11 cm³\]
Quel est le volume d'un seau en forme de cône tronqué ?
Considérons un seau pour enfant ayant les dimensions suivantes :
- Diamètre haut : 18,5 cm (donc rayon R₁ = 9,25 cm).
- Diamètre bas : 12 cm (donc rayon R₂ = 6 cm).
- Hauteur : 15 cm.
Calcul du volume :
Le volume d’un cône tronqué est donné par la formule :
\[ V = \frac{1}{3} \pi h \left( R_1^2 + R_1 R_2 + R_2^2 \right) \]
Substituons les valeurs :
- h : 15 cm
- R₁ : 9,25 cm
- R₂ : 6 cm
Volume = \[ \frac{1}{3} \pi \times 15 \times \left( 9,25^2 + 9,25 \times 6 + 6^2 \right) \]
Volume = \[ \frac{1}{3} \pi \times 15 \times \left( 85,5625 + 55,5 + 36 \right) \]
Volume = \[ \frac{1}{3} \pi \times 15 \times 177,0625 \]
Volume = \[ \pi \times 885,3125 / 3 \]
Volume ≈ \(3,14159 \times 295,1042 ≈ 927,1 \, \text{cm}^3\).
Conversion en litres :
Comme 1 litre = 1000 cm³ :
- Volume = 2781,29 cm³ ≈ 2,8 litres
Rappel de la formule dérivée :
On peut retrouver la formule d’un cône tronqué en partant de la formule du volume d’un cône :
\[ V = \frac{\pi R_1^2 h_1}{3} - \frac{\pi R_2^2 h_2}{3} \]En posant \( h = h_1 - h_2 \), on simplifie la formule pour obtenir :
\[ V = \frac{1}{3} \pi h \left( R_1^2 + R_1 R_2 + R_2^2 \right) \]J'ai acheté un arbre en grume (tronc) la base fait 0.40 m de diamètre, et à l'autre bout 0.30 m de diamètre le tronc fait 5 mètres de long. Pouvez-vous me calculer le volume ou le cubage svp, car j'ai quitter l'école le jour de mes 16 ans et j'ai tout oublié merci.
Le 27-05-2013
Réponse : Bonjour, la grume fait 0,48 m3 en utilisant l'outil de cette page et avec les rayons (déduits des diamètres donnés) R1 = 0.20 et R2 = 0.15.
C'était très bien d'identifier dans une grume (le tronc d'un arbre abattu) un cône tronqué, et en appliquant la formule de cette page, nous pouvons estimer précisément son volume. Mais, en fait pour estimer le volume des grumes, les bucherons ne procèdent pas de cette manière (trop compliquée et inutile). Ils se contentent de prendre le diamètre au milieu de la grume et d'appliquer la formule du volume d'un cylindre droit. L'écart est très faible du fait de la longueur des grumes par rapport à l'écart des diamètres.
Le diamètre en question est égal à la moyenne arithmétique de 0.40 et 0.30 soit :
(0.40 + 0.30) ÷ 2 = 0.35 m.
Calculons le volume d'un cylindre de diamètre 0.35 m (donc de rayon 0.175 m) et de longueur 5 m :
π × 0.1752 × 5 = 0.481056375 m3
Nous pouvons comparer avec le résultat obtenu avec le volume du cône tronqué :
(5 × π ÷ 3) × ( 0.202 + 0.152 + 0.20×0.15) = 0.484328867 m3
Ecart : 0.484328867 − 0.481056375 = 0,003272492 m3 , soit moins de 3.3 Litres !!!