Rechercher un outil (en entrant un mot clé):
Volume d'un segment sphérique
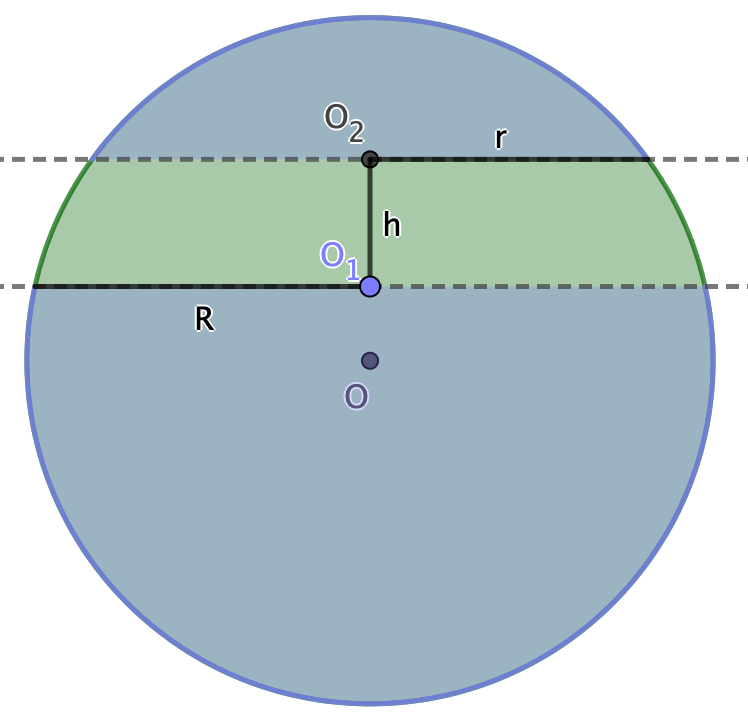
Un segment sphérique est une portion d'une sphère délimitée par deux plans parallèles qui coupent la sphère en formant deux disques circulaires.
Formule du volume :
Le volume d'un segment sphérique est donné par la formule :
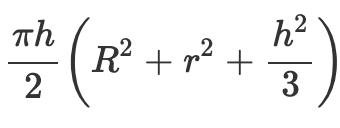
Cette formule prend en compte :
- R : Le rayon de la sphère.
- h : La hauteur du segment, c'est-à-dire la distance entre les deux plans parallèles.
Calculer le volume d'un segment sphérique :
Le résultat est arrondi à 10-6 près et l'unité du volume est celle du rayon et de la hauteur au cube. Exemple : si le rayon s'exprime en m, alors le volume de la calotte sphérique s'exprime en m3.
Définition :
- Imaginez une sphère complète, comme une balle.
- Deux plans parallèles traversent cette sphère, créant une tranche ou segment.
- Cette portion de sphère, enfermée entre les deux coupes, est appelée le segment sphérique.
Les disques formés par les coupes dépendent de la position des plans par rapport au centre de la sphère :
- Plus les plans sont proches du centre, plus les disques sont grands.
- Plus les plans sont éloignés, plus les disques sont petits.
Exemple de calcul :
Soit une sphère de rayon R = 10 cm et un segment de hauteur h = 6 cm. Calculons son volume :
- Formule : Volume = `πh²(3R - h) / 3`
- Substitution : Volume = `π × 6² × (3 × 10 - 6) / 3`
- Calcul : Volume = `π × 36 × (30 - 6) / 3` = `π × 36 × 24 / 3` = `π × 288`
- Résultat : Volume ≈ `3,14159 × 288 ≈ 904,78 cm³`
Résumé :
Un segment sphérique est une portion de sphère délimitée par deux disques parallèles. Il constitue une forme importante en géométrie pour le calcul des volumes. La formule du volume d’un segment sphérique est essentielle dans les sciences et les applications pratiques.
Voir la page suivante :
Démonstration de la formule et exemples de calculs.

