Rechercher un sujet parmi les questions (en entrant un mot clé):
Quel est le volume d'un segment sphérique ?
Comment calculer le volume d'un segment sphérique ? Nous donnerons la démonstration de la formule.
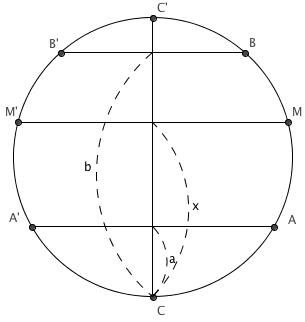
Considérons une sphère de diamètre CC' = 2R; coupons-la par deux plans AA' et BB' perpendiculairement à CC' et proposons nous d'évaluer le volume du segment entre ces deux plans.
Publié le 17/02/2013 à 21:46:42 - Auteur : Webmaster
REPONSES :
Soit un plan MM' parallèle aux plans AA' et BB' et compris entre eux. Soient a,b et x les distances des plans AA', BB' et MM' à C.
L'intersection du plan MM' avec la sphère est un cercle de rayon y. Déterminons la mesure du carré son rayon et ainsi nous aurons son aire S = πy².
Appliquons le théorème de Pythagore dans les triangles rectangles. CMC' est rectangle puisque CC' est un diamètre.
y² + (2R − x)² + y² + x² = (2R)²
2y² = (2R)² − (2R − x)² − x²
2y² = (2R)² − (2R)² + 2(2R)x − x² − x²
2y² = 2(2R)x − 2x²
y² = (2R)x − x²
y² = x(2R − x)
on a S(x) = π(2Rx − x²)
Le volume du segment sphérique est égale ∫abπ(2Rx − x²)dx.
Une primitive F de S est égale à F(x) = π(Rx² − x³/3) et le volume de segment sphérique VAA'BB' est égal à : F(b) − F(a).
VAA'BB' = π(Rb² − b³/3) − π(Ra² − a³/3) = π(Rb² − b³/3 − Ra² + a³/3) = π[R(b² − a²) −1/3(b³ − a³)]
VAA'BB' = π(b − a)[R(b + a) − 1/3(b² + ab + a²)]
Désignons par r et r' les rayons des deux bases et par h leur distance. On a :
b − a = h et en appliquant Pythagore (comme précédemment pour y) on a r² = a(2R − a) et r'² = b(2R − b).
De là r² + r'² = a(2R − a) + b(2R − b) = 2R(a + b) − a² − b² alors R(b+a) = ½(r² + r'² + a² + b²)
On remplace dans l'expression de VAA'BB' b − a par h, R(b+a) par ½(r² + r'² + a² + b²)
VAA'BB' = πh[½(r² + r'² + a² + b²) −1/3(b² + ab + a²)]
VAA'BB' = πh[½(r² + r'²) + 3/6(a² + b²) −2/6(a² + b²) −2/6ab]
VAA'BB' = πh[½(r² + r'²) + (a² − 2ab + b²)÷6]
VAA'BB' = πh[½(r² + r'²) + (a− b)²÷6]
VAA'BB' = ½πh[(r² + r'²) + h²÷3] ou encore :
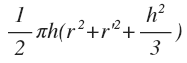
On retrouve bien la formule du volume d'un segment sphérique donnée en géométrie.
Réponse publiée le 17/02/2013 à 23:04:21 - Auteur : Webmaster

