Rechercher un outil (en entrant un mot clé):
L'ellipsoïde
Un ellipsoïde est une surface fermée symétrique, dont chaque section plane est une ellipse ou un cercle. C'est une généralisation de la sphère, mais avec des axes de longueurs différentes. Un ellipsoïde est défini par trois axes principaux : le grand axe, le moyen axe et le petit axe, qui sont perpendiculaires entre eux.
Le volume contenu dans une ellipsoïde peut être calculé à l'aide de la formule :
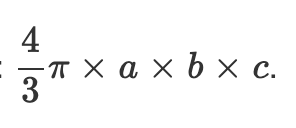, où a, b,
et c sont les demi-longueurs des trois axes principaux.
Une ellipsoide a pour équation cartésienne :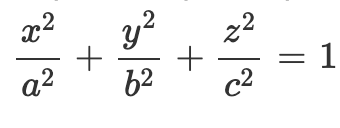 
,
avec a le demi grand axe, superieur au demi moyen axe b, superieur demi petit axe c.
Calculer le volume d'une ellipsoide :
Le résultat est arrondi à 10-6 près et l'unité du volume est celle du rayon et de la hauteur au cube. Exemple : si le rayon s'exprime en m, alors le volume de la calotte sphérique s'exprime en m3.
Propriétés d'une ellipsoïde
Une des propriétés majeures d'un ellipsoïde est que chaque section par un plan qui passe par un de ses axes est une ellipse. Si les trois axes de l'ellipsoïde sont égaux, on obtient une sphère. En revanche, si deux axes sont égaux et le troisième différent, on parle alors d'un ellipsoïde de révolution.
L'ellipsoïde a de nombreuses applications en géométrie, en physique et en astronomie. Par exemple, la Terre est souvent approximée par un ellipsoïde, car elle est légèrement aplatie aux pôles et renflée à l'équateur, ce qui donne une forme plus proche de l'ellipsoïde de révolution.
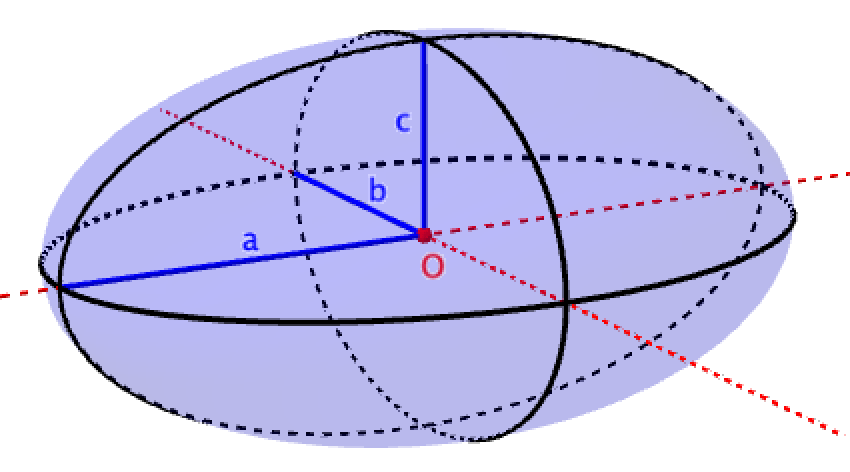
Le volume d'une ellipsoide est donné par la formule : `V = 4/3 π a b c`.
Remarques :
Si a = b ou b = c, alors l'ellipsoïde est une ellipsoïde de révolution.
Si a = b, alors l'ellipsoïde de révolution aplati a une forme de galet.
Si b = c, alors l'ellipsoïde de révolution allongé a une forme de ballon de rugby.
Si a = b = c, alors l'ellipsoïde est une sphère.
