Rechercher un outil (en entrant un mot clé):
Calcul des volumes (et formules des volumes) de :
Calculer le volume d'un cône
Le volume d'un cône de révolution est égal à un tiers de l’aire de sa base multipliée par la hauteur du cône h.
Si la base d'un cône est un disque de rayon R son aire est égale à : π × R2.
alors la formule du volume du cône est égal à : π × R2 × h ÷ 3 ou encore :
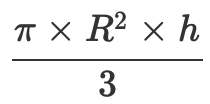
* Entrer les valeurs dans la même unité.
Le volume du cône s'exprimera dans l'unité au "cube" des mesures. Par exemple, si vous choisissez d'exprimer leurs valeurs en cm, la valeur du volume obtenue s'exprimera en cm3.
Cône de réolution
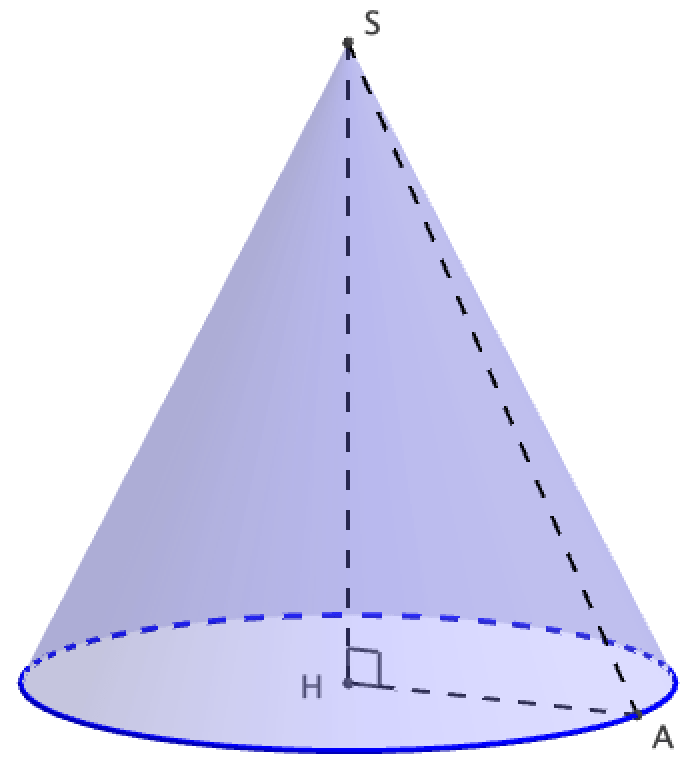
- Un cône de révolution est un solide obtenu par la rotation d'un triangle rectangle autour de l'un des ses côtés de son angle droit.
- La hauteur du cône est la distance entre le sommet S et le centre de sa base ici dans la figure (ici H sur la figure).
- La droite (SH) , prolongation de la hauteur du cône de révolution de la figure, est perpendiculaire au plan défini par la base du cône. On dit que le sommet du cône est "à la verticale" du centre du disque de base..
Quel est le volume d'un cône de signalisation ?
La hauteur d'un cône de signalisation est de 50 cm et sa base a pour diamètre 29 cm. Quel est son volume ?
Le raton de la base est égal à 29 ÷ 2 = 14.5 cm.
L'aire de la base est égale en cm2 à : π × R2 = π × 14.52 = π × 210.25 = 660.52 cm2
Le volume est égal en cm3 à : 660.52 × 50 ÷ 3 = 11 008.7 cm3, soit en dm3 environ 11 dm3, soit encore 11 litres.
