Rechercher un outil (en entrant un mot clé):
voir aussi : calculer le volume d'un cône
Calculer l'aire de la surface latérale d'un cône
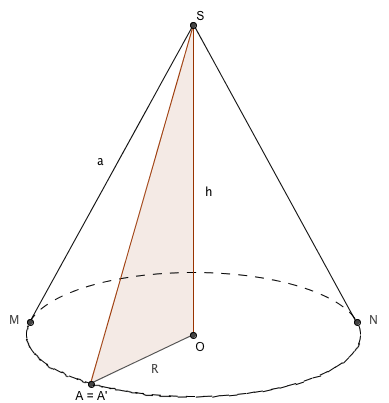
Considérons un cône de révolution dont la base est un disque de rayon R. Ce type de cône est défini par sa base circulaire et son sommet situé à la verticale de cette base.
L'aire de la surface latérale S de ce cône, après son développement à plat, est donnée par la formule : S = π × R × a, où a est l'apothème du cône. L'apothème est la distance entre le sommet du cône et un point sur le bord de la base.
Si au lieu de l'apothème, vous connaissez la hauteur h du cône, la formule change légèrement. La hauteur est la distance perpendiculaire entre le sommet du cône et le centre de la base. Dans ce cas, l'apothème peut être calculé à l'aide du théorème de Pythagore car il forme un triangle rectangle avec le rayon R et la hauteur h. Ainsi, l'apothème a est égal à √(R² + h²), et l'aire de la surface latérale devient :
S = π × R × √(R² + h²).
En résumé :
- Si vous connaissez l'apothème : S = π × R × a
- Si vous connaissez la hauteur : S = π × R × √(R² + h²)
Ces formules permettent de calculer l'aire de la surface latérale du cône de manière précise, que vous connaissiez l'apothème ou la hauteur.
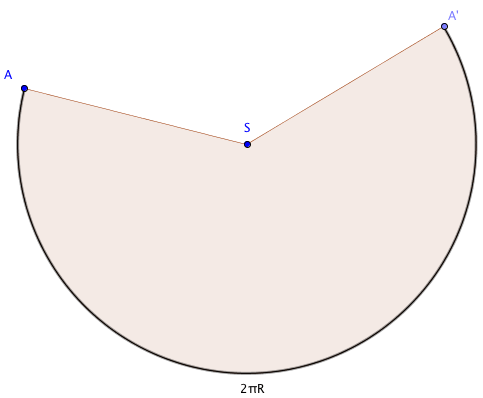
Pour obtenir le développement de la surface latérale d'un cône il suffit de fendre le cône selon SA (un apothème du cône ). L'arc de cercle AA' est égal à 2πR.
Calcul de la surface d'un cône :
Soit un cône de révolution de hauteur égale à 10 cm et dont le rayon de sa base R est égal à 7 cm. Calculons l'aire de sa surface latérale.
Nous pouvons calculer la mesure son apothème puisque utiliser la seconde formule revient à le faire.
La valeur de a est égale à : √(102 + 72) = √149 ≈ 12.20655.
S est alors égale à : S = π × 7 × √149 ≈ 268.44 cm2 à 10-2 près.

