Rechercher un outil (en entrant un mot clé):
Calculer l'aire de la surface d'un polygone régulier
Un polygone régulier (convexe) est un un polygone (figure à plusieurs côtés) dont tous ses côtés ont la même longueur et tous ses angles ont la même mesure.
Par conséquence l'aire d'un polygone régulier ne dépend que du nombre de côtés et de la valeur de la longueur de l'un d'eux.
Aire = `\dfrac{n × c^2} {4 × \tan (180^{\circ}/{n})}` (démonstration)
Calcul de la surface d'un pentagone (5 côtés) :
Formule de l'aire d'un pentagone = `\dfrac{5 × c^2} {4 × \tan ({180^{\circ}}/{5})}`
Formule de l'aire d'un pentagone = `5/4 \times \dfrac{c^2} {\tan (36^{\circ})}`
Aire d'un hexagone (6 côtés) :
Formule de l'aire d'un hexagone = `{6 × c^2} / {4 × \tan ({180^{\circ}}/{6})}`
= `3/2 \times \dfrac{c^2} {\tan (30^{\circ})}`
= `3/2 \times \dfrac{c^2} {\sqrt{3}/3}`
= `\dfrac{3\sqrt{3}}{2} \times c^2`
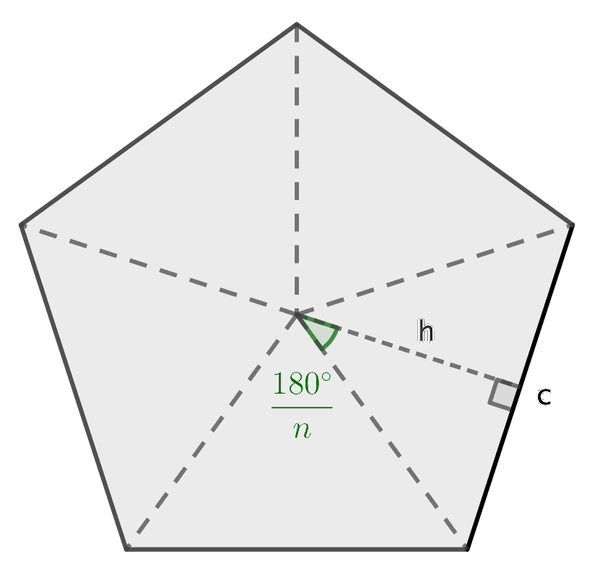
Démonstration forme générale :
Aire polygone régulier = n × Aire du triangle
Aire du triangle = `\dfrac{c \times h} {2} `
`\tan({180^{\circ}}/{n}) = {c/2}/{h} `
`h = \dfrac{c/2}{\tan({180^{\circ}}/{n})}`
`h = \dfrac{c \times n }{2 \times \tan({180^{\circ}}/{n})}`
D'où
Aire `=\dfrac {n \times c \times c}{2 \times 2 \times \tan({180^{\circ}}/{n})}`
Aire `= \dfrac{n \times c^2}{4 \times \tan({180^{\circ}}/{n})}`
La formule est valable pour tous les polygones réguliers : le triangle équilatéral (3 côtés de la même longueur); le carré (4 côtés); le pentagone (5 côtés); l'hexagone (6 côtés); l'heptagone (7 côtés); l'octogone (8 côtés); l'ennéagone (9 côtés); le décagone (10 côtés); l'hendécagone (11 côtés); le dodécagone (12 côtés)

