Rechercher un outil (en entrant un mot clé):
voir aussi : calculer le volume d'un cylindre
Calculer l'aire de la surface latérale d'un cylindre
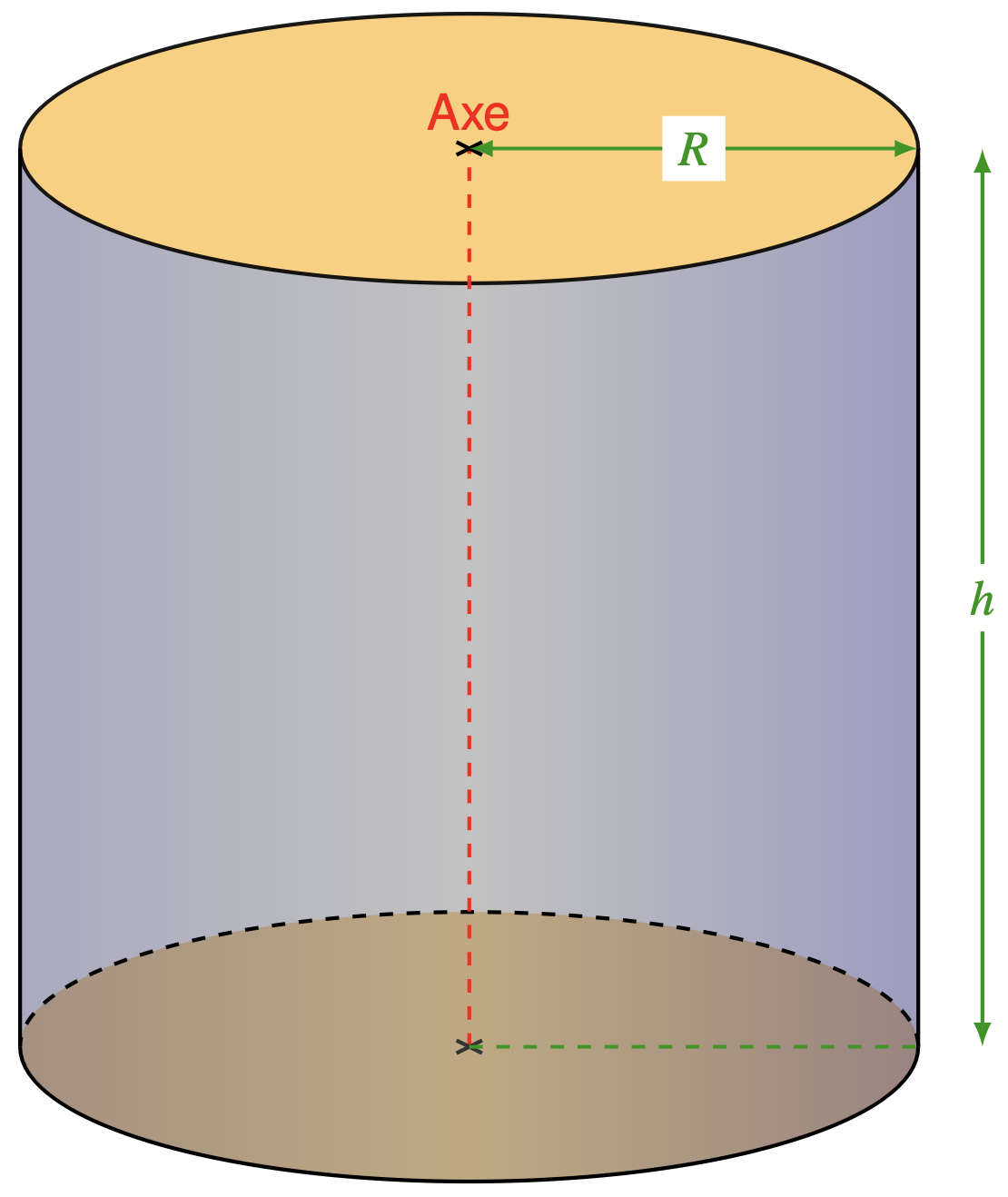
Considérons un cylindre de révolution, dont la base est un disque de rayon R et qui possède une hauteur h. Un cylindre de révolution est défini par ses deux bases circulaires parallèles et une surface latérale perpendiculaire aux bases.
L'aire de la surface latérale S du cylindre correspond à la surface qui, une fois déroulée, forme un rectangle. La largeur de ce rectangle est égale à la hauteur du cylindre h, tandis que sa longueur est égale au périmètre de la base circulaire, soit 2πR.
Par conséquent, l'aire de la surface latérale est donnée par la formule :
S = 2π × R × h, où R est le rayon de la base du cylindre et h est la hauteur du cylindre.
En résumé :
- R : Rayon de la base circulaire du cylindre.
- h : Hauteur du cylindre, c'est-à-dire la distance entre les deux bases.
- S : Aire de la surface latérale du cylindre, obtenue avec la formule S = 2π × R × h.
Cette formule vous permet de calculer l'aire de la surface latérale du cylindre, essentielle pour diverses applications géométriques et pratiques.
Calcul de la surface d'un cylindre :
Un cylindre R = 4 cm et de hauteur h = 7 cm.
L'aire de sa surface latérale est égale à : `2 × π × 4 × 7 = 175,292919 cm²`