Calculis

Calculer l'aire (de la surface) d'un segment de disque

Un segment de disque est une portion de disque délimitée par :

• Une corde [AB] du cercle.
• L’arc de cercle AB situé au-dessus (ou en dessous) de cette corde.

Le cercle a :

• O : pour centre.
• R : pour rayon.

Formule de l'aire du segment :

L'aire d'un segment est obtenue en soustrayant l'aire du triangle isocèle OAB de l'aire du secteur angulaire correspondant :

Aire du segment = Aire du secteur angulaire - Aire du triangle isocèle OAB

Formule avec l’angle α en degrés :

`Aire_{segment} = (π × α × R²) / 360 - (1/2 × R² × sin(α))`

où :

• α : l’angle au centre, exprimé en degrés, et `α ≤ 180°`.
• R : le rayon du cercle.

Formule avec l’angle α en radians :

`Aire_{segment} = (1/2 × α × R²) - (1/2 × R² × sin(α))`

ou :

`Aire_{segment} = 1/2 × R² × (α - sin(α))`

où :

• α : l’angle au centre, exprimé en radians, et `α ≤ π`.

Il suffit de rentrer 2 valeurs sur 4.

L'aire s'exprimera dans l'unité au "carré" du rayon du disque ou des longueurs données. Par exemple si vous choisissez d'exprimer sa valeur en cm, la valeur de l'aire obtenue s'exprimera en cm².

Aire et propriétés géométriques d'un secteur circulaire

Aire du triangle isocèle OAB :

L'aire d'un triangle isocèle formé par deux rayons et une corde peut être calculée avec la formule :

`Aire_{OAB} = 1/2 R^2 \sin(\alpha)`

Démonstration :

1. Dans le triangle rectangle OHA, avec OH = R - h, on a :
• `(R - h) = R \cos(\alpha / 2)`
• `AB / 2 = R \sin(\alpha / 2)`
2. La formule de l'aire du triangle est :

`Aire_{OAB} = 1/2 (R - h) \times AB`

3. En substituant, on obtient :

`Aire_{OAB} = R^2 \cos(\alpha / 2) \sin(\alpha / 2)`

4. En utilisant l'identité trigonométrique `\sin(a) \cos(b) = 1/2 [ \sin(a + b) + \sin(a - b) ]` avec `a = b = \alpha / 2` :

`Aire_{OAB} = 1/2 R^2 \sin(\alpha)`

Longueur de la corde :

La longueur de la corde en fonction :

• Du rayon R et de l'angle α :

`c = 2R \sin(\alpha / 2)`

• Du rayon R et de la flèche h :

`c = 2\sqrt{(2R - h)h}`

Démonstration :

1. En appliquant le théorème de Pythagore :

`c / 2 = \sqrt{R^2 - (R - h)^2}`

`c = 2\sqrt{R^2 - (R - h)^2}`

2. En développant :

`c = 2\sqrt{R^2 - [R^2 - 2Rh + h^2]}`

`c = 2\sqrt{2Rh - h^2}`

`c = 2\sqrt{h(2R - h)}`

Rayon du secteur angulaire :

La formule du rayon en fonction de la flèche h et de la longueur de la corde c est :

`R = (4h^2 + c^2) / (8h)`

Démonstration :

1. En appliquant le théorème de Pythagore :

`R^2 - (R - h)^2 = c^2 / 4`

`h(2R - h) = c^2 / 4`

2. En réarrangeant :

`2R = c^2 / (4h) + h`

`R = (c^2 / 8h) + h / 2`

`R = (4h^2 + c^2) / (8h)`

Flèche (Hauteur) h :

La hauteur h en fonction du rayon R et de la corde c est :

`h = R - \sqrt{R^2 - (c^2 / 4)}`

Démonstration :

1. En appliquant le théorème de Pythagore :

`c^2 / 4 + (R - h)^2 = R^2`

`(R - h)^2 = R^2 - c^2 / 4`

`R - h = \sqrt{R^2 - c^2 / 4}`

`h = R - \sqrt{R^2 - c^2 / 4}`

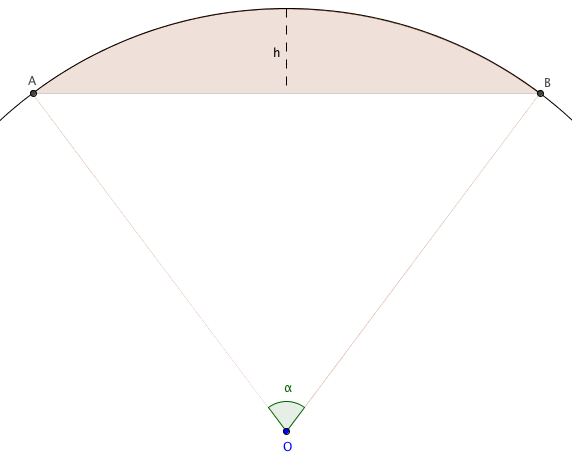
Illustration :

Voici une représentation graphique d'un segment de disque pour mieux comprendre les relations géométriques :