Calculis

Calculer l'aire (de la surface) d'un triangle quelconque

Un triangle est une figure plane qui possède 3 côtés. Soit un triangle de base B et de hauteur h.

Son aire est égale à la moitié du produit la longueur de sa base par la hauteur issue du sommet opposé à cette base, soit :

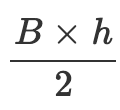
L'aire s'exprimera dans l'unité au "carré" des valeurs du triangle. Par exemple si vous choisissez d'exprimer ces valeurs en cm, la valeur de l'aire obtenue s'exprimera en cm²

Calcul de l'aire d'un triangle

Un triangle, dont la base a pour longueur 7 cm et dont la hauteur a pour hauteur 3 cm, possède une aire égale à :

7 × 3 ÷ 2 = 10.5 cm².

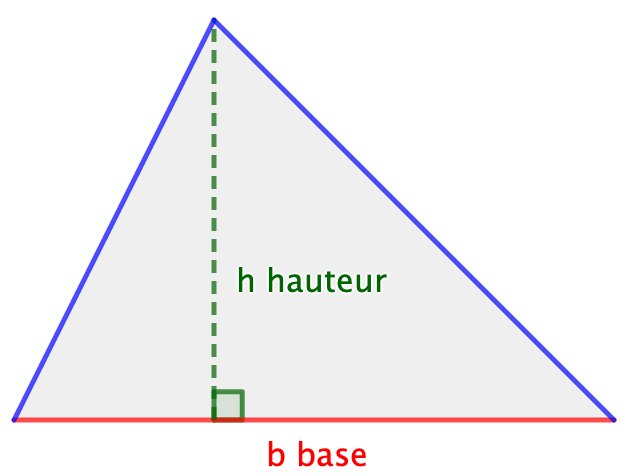
Calculer l'aire (de la surface) d'un triangle équilatéral

Le triangle équilatéral possède trois côtés égaux. On peut facilement calculer une hauteur grâce au théorème de Pythagore. En effet, si on désigne par c la mesure d'un côté, alors on a :

c² = h² + c²/4

c² − c²/4 = h²

3c²/4 = h²

et de là h = √3 × c/2

Nous obtenons la hauteur en fonction de la mesure des côtés, en remplaçant la hauteur par √3.c/2 et la base par c dans la formule générale de l'aire du triangle.

On obtient la formule de l'aire d'un triangle équilatéral seulement en fonction de la mesure c d'un de ses côtés :

c × √3 × c ÷ 2 ÷ 2 = √3 × c² ÷ 4.

Aire d'un triangle équilatéral de côté c :

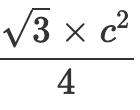
Calculons l'aire d'un triangle équilatéral dont la mesure des côtés est égale à 2 :

√3 × 2² ÷ 4 = √3 × 4 ÷ 4 = √3.