Calculis

Calculer l'aire de la surface latérale d'une pyramide régulière tronquée

Une pyramide régulière tronquée est une pyramide dont le sommet est coupé par un plan parallèle à la base. Elle possède deux bases parallèles :

• B : la base inférieure (plus grande).
• b : la base supérieure (plus petite).

Formule de l'aire latérale :

Pour une pyramide régulière tronquée, l'aire de la surface latérale S est donnée par la formule :

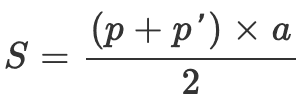
où :

• p : périmètre de la base inférieure (B).
• p' : périmètre de la base supérieure (b).
• a : apothème de la pyramide tronquée (distance oblique entre les deux bases).

Explications :

Cette formule s’appuie sur la moyenne des périmètres des deux bases et la hauteur oblique (a) pour calculer la surface latérale. La surface latérale est donc la somme des aires des trapèzes formés par les côtés de la pyramide tronquée.

Les mesures données doivent être exprimées dans la même unité.

Exemple de calcul :

Soit une pyramide régulière tronquée avec :

• Périmètre de la base inférieure (p) : 20 cm.
• Périmètre de la base supérieure (p') : 12 cm.
• Apothème (a) : 8 cm.

Son aire latérale est calculée comme suit :

S = [(p + p') / 2] × a

S = [(20 + 12) / 2] × 8

S = [32 / 2] × 8

S = 16 × 8 = 128 cm²

Applications :

Le calcul de l'aire latérale d'une pyramide tronquée est utile pour :

• Estimer la quantité de matériaux nécessaires pour recouvrir une pyramide tronquée.
• Analyser les surfaces dans des projets de design ou d'architecture.
• Calculs en géométrie pour des simulations 3D ou des modèles physiques.

Exemple d'une pyramide tronquée régulière à base carrée

Considérons une pyramide tronquée régulière à base carrée. Voici sa représentation :

Calcul de la surface latérale :

Soit une pyramide tronquée à base carrée avec :

• Côté de la grande base : 8 cm.
• Côté de la petite base : 4 cm.
• Hauteur verticale (h) : 10 cm.

Étape 1 : Calcul des périmètres

Les périmètres des bases sont :

• Périmètre de la grande base (p) : 4 × 8 = 32 cm.
• Périmètre de la petite base (p') : 4 × 4 = 16 cm.

Étape 2 : Calcul de l'apothème (a)

Utilisons le théorème de Pythagore pour calculer l'apothème :

a = √[h² + ((c - c') / 2)²]

a = √[10² + ((8 - 4) / 2)²]

a = √[10² + (4 / 2)²]

a = √[100 + 2²]

a = √[100 + 4] = √109

Étape 3 : Calcul de la surface latérale (S)

La formule de la surface latérale est :

S = [(p + p') / 2] × a

Substituons les valeurs :

S = [(32 + 16) / 2] × √109

S = [48 / 2] × √109

S = 24 × √109

En approximant √109 ≈ 10,44 :

S ≈ 24 × 10,44 = 250,56 cm²

Conclusion :

La surface latérale de cette pyramide tronquée est d’environ 250,56 cm².