Rechercher un outil (en entrant un mot clé):
Calculer l'aire d'un secteur sphérique
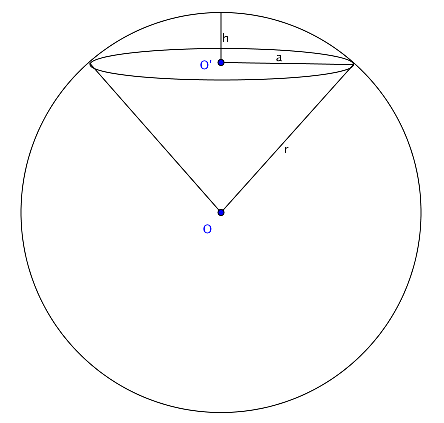
Un secteur sphérique est une portion de la surface d'une sphère délimitée par une hauteur h. Soit :
- O : le centre de la sphère.
- r : le rayon de la sphère.
- h : la hauteur du secteur sphérique (distance perpendiculaire depuis la base circulaire jusqu’au sommet).
Formule de l'aire :
L'aire de la surface du secteur sphérique est donnée par la formule :
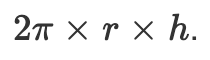
ou sous forme textuelle :
Aire = `2π × r × h`
Calcul du rayon apparent du secteur sphérique :
Le rayon apparent a du secteur sphérique est donné par la formule :
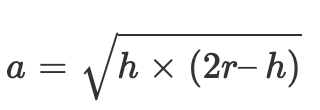
ou sous forme textuelle :
a = `√[r² - (r - h)²]`
L'aire s'exprimera dans l'unité au "carré" du rayon de la sphère. Par exemple, si vous choisissez d'exprimer sa valeur en cm, la valeur de l'aire obtenue s'exprimera en cm2.
Exemple de calcul :
Soit une sphère avec :
- Rayon (r) = 10 cm.
- Hauteur (h) = 4 cm.
Étape 1 : Calcul de l’aire du secteur sphérique
Utilisons la formule :
Aire = `2π × r × h`
Aire = `2π × 10 × 4`
Aire = `80π`
En approximant `π ≈ 3,14159` :
Aire ≈ `80 × 3,14159 = 251,33 cm²`
Étape 2 : Calcul du rayon apparent (a)
Utilisons la formule :
a = `√[r² - (r - h)²]`
a = `√[10² - (10 - 4)²]`
a = `√[100 - 6²]`
a = `√[100 - 36]`
a = `√64 = 8 cm`
Conclusion :
L'aire de ce secteur sphérique est d’environ 251,33 cm² et son rayon apparent est 8 cm.