Calculis

voir aussi : calculer le volume d'un cône tronqué

Calculer l'aire de la surface latérale d'un cône tronqué

Un cône tronqué est obtenu en coupant un cône par un plan parallèle à sa base. La base reste un disque de rayon R, et la petite base (ou section supérieure) est un disque de rayon r.

Formule de l’aire latérale :

L'aire de la surface latérale S du développement d'un cône tronqué est donnée par :

`S = π × (R + r) × a`

où :

• R : rayon de la base du cône.
• r : rayon de la petite base (section supérieure).
• a : apothème du cône tronqué (la distance oblique entre les deux bases).
• π : constante mathématique (≈ 3,14159).

Illustration :

Voici une représentation d’un cône tronqué pour mieux comprendre les dimensions impliquées :

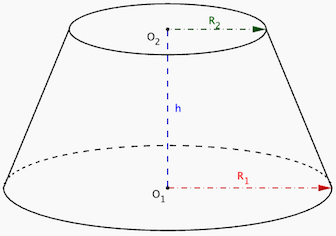
Exemple de calcul :

Considérons un cône tronqué avec :

Pour faire apparaître les formules correctement utilisez l'outil une fois.

• Rayon de la base : R = 8 cm
• Rayon de la petite base : r = 5 cm
• Apothème : a = 10 cm

L'aire latérale est calculée comme suit :

`S = π × (R + r) × a`

`S = π × (8 + 5) × 10`

`S = π × 13 × 10 = 130π`

En approximant π ≈ 3,14159 :

`S ≈ 130 × 3,14159 = 408,41 cm²`

Applications :

Le calcul de la surface latérale d’un cône tronqué est utile dans divers contextes, comme :

• La conception et l’analyse de pièces mécaniques.
• La réalisation de modèles 3D ou d’objets en design industriel.
• Les calculs en architecture ou en arts visuels (modèles de cônes tronqués).

Calcul de la surface latérale d'un cône tronqué

Pour obtenir le développement de la surface latérale d'un cône tronqué, il suffit de fendre le cône selon une de ses apothèmes (A'A). L'arc de cercle résultant (AB) a une longueur égale à 2πR, où R est le rayon de la base du cône.

Calcul de l’apothème :

L’apothème a peut être calculé à l’aide de la relation suivante :

`a = √[h² + (R – r)²]`

• h : hauteur du cône tronqué (distance perpendiculaire entre les deux bases).
• R : rayon de la base principale.
• r : rayon de la base supérieure.

Exemple de calcul :

Soit un cône tronqué dont :

• Hauteur : h = 16 cm.
• Rayons des bases : R = 25 cm et r = 13 cm.

Étape 1 : Calculons l’apothème a :

`a = √[16² + (25 – 13)²]`

`a = √[16² + 12²] = √[256 + 144] = √400 = 20 cm`

Étape 2 : Calculons la surface latérale S :

`S = π × (R + r) × a`

`S = π × (25 + 13) × 20`

`S = π × 38 × 20 = 2387,61 cm²` (arrondi à 10^-2 près).

Illustrations :

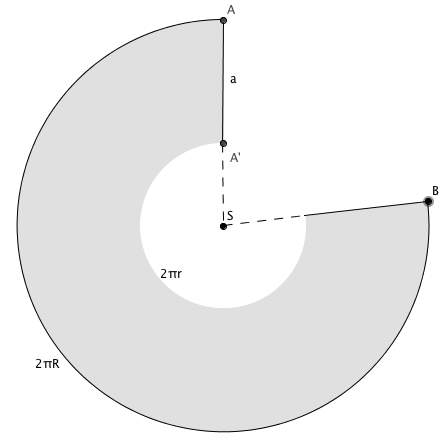
Développement de la surface latérale d'un cône tronqué.

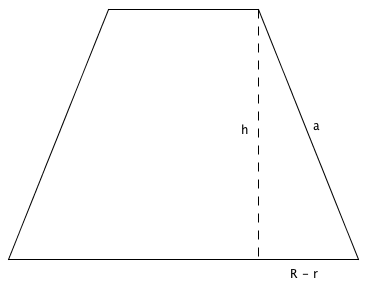
Coupe d'un cône tronqué montrant ses dimensions.