Calculis

Calculer l'aire de la surface d'une ellipse

Une ellipse est une figure géométrique plane définie par deux axes principaux :

• Le demi-grand axe (a) : la moitié de la longueur de l'axe le plus long.
• Le demi-petit axe (b) : la moitié de la longueur de l'axe le plus court.

Les foyers de l'ellipse, notés `F_1` et `F_2`, sont deux points fixes situés sur l'axe principal.

Formule de l’aire :

L’aire d’une ellipse est donnée par la formule suivante :

Aire = `π × a × b`

Où :

• a : demi-grand axe.
• b : demi-petit axe.
• π : constante mathématique, environ égale à 3,14159.

Remarque :

La surface d’un disque est donnée par la formule `π × r²`, où r est le rayon. Pour une ellipse, le carré du rayon est remplacé par le produit du demi-grand axe (a) et du demi-petit axe (b).

L'aire s'exprimera dans l'unité au "carré" du rayon du disque ou des longueurs données. Par exemple si vous choisissez d'exprimer sa valeur en cm, la valeur de l'aire obtenue s'exprimera en cm².

Exemple :

Soit une ellipse avec :

• a = 10 cm (demi-grand axe).
• b = 5 cm (demi-petit axe).

Son aire est calculée comme suit :

Aire = `π × a × b`

Aire = `π × 10 × 5`

Aire = `50π`

En approximant π ≈ 3,14159 :

Aire ≈ `50 × 3,14159 = 157,08 cm²`

Applications :

Le calcul de l'aire d'une ellipse est utile dans divers contextes, comme :

• L’analyse des formes elliptiques en architecture et design.
• Les calculs dans les modèles astronomiques (par exemple, les orbites elliptiques).
• Les mesures de surfaces dans des applications géométriques complexes.

Propriétés d'une ellipse

Une ellipse est caractérisée par ses deux axes principaux :

• Demi-grand axe (a) : La moitié de la longueur de l'axe principal.
• Demi-petit axe (b) : La moitié de la longueur de l'axe secondaire.

La distance focale, notée f, est calculée à l’aide de la formule :

`f = √(a² - b²)`

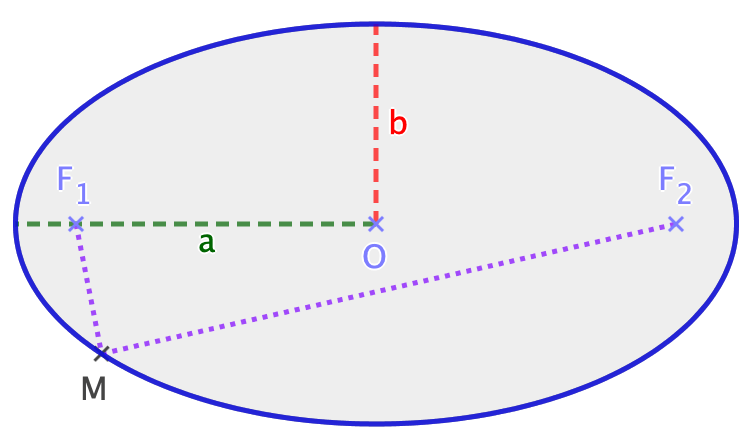
Tracer une ellipse avec une corde

La propriété fondamentale d'une ellipse est que la somme des distances entre un point M sur l'ellipse et les deux foyers F₁ et F₂ est constante :

MF₁ + MF₂ = 2a

Cette propriété peut être utilisée pour tracer une ellipse parfaite :

1. Fixez deux piquets aux points correspondant aux foyers F₁ et F₂.
2. Attachez une corde dont la longueur est égale à 2a (longueur du grand axe).
3. À l’aide d’un crayon maintenu tendu par la corde, dessinez l’ellipse en déplaçant le crayon autour des foyers.

Ce procédé est idéal pour des applications pratiques, comme dessiner un parterre de fleurs.

Périmètre d'une ellipse

Le périmètre d'une ellipse est plus complexe à déterminer que celui d'un cercle. Cependant, une approximation célèbre, proposée par le mathématicien Srinivasa Ramanujan, est donnée par :

`π[3(a + b) - √((3a + b)(a + 3b))]`

Applications :

Cette approximation est souvent utilisée dans des calculs pratiques pour des ellipses où une exactitude parfaite n'est pas nécessaire, comme :

• Calculs en design industriel ou architecture.
• Évaluation des longueurs pour des parcours elliptiques.
• Applications en physique ou en ingénierie.