Rechercher un outil (en entrant un mot clé):
Calcul de périmètre (et formules des périmètres) de :
Calculer le périmètre d'une ellipse
Le calcul du périmètre d'une ellipse n'est pas du tout facile. Souvent vous trouvez (sur internet) des formules qui sont données pour exactes, alors qu'elles ne donnent que des approximations plus ou moins éloignées de la valeur exacte.
L'outil proposé ici utilise les deux formules. la première (dite classique) donne une estimation grossière de la valeur du périmètre (une erreur de 1%) et la seconde : la formule n°2 du célèbre mathématicien Ramanujan qui donne une valeur jusqu'à 12 chiffres significatifs (très largement suffisante pour un outil en ligne).
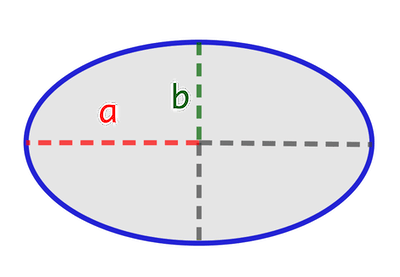
`a` représente de demi-grand axe.
`b` représente de demi-petit axe.
Les formules du périmètre d'une ellipse
Formule classique : `p \approx` `2\pi\sqrt((a^2 + b^2)/2)`
Cette formule donne le périmètre avec une erreur d'environ 1%. Cela peut paraître peu, mais pour des valeurs supérieures à 10, seul 1 seul chiffre peut être exact !
Si les valeurs de a et b sont proches, la formule donne une bonne approximation du périmètre.
Formule n°1 de Ramanujan : `p \approx` `π ( 3(a + b) - \sqrt[(3a + b)(a + 3b)] )`
Cette formule donne le périmètre avec une erreur inférieure à 0,01%.
Formule n°2 de Ramanujan : `p \approx` `π(a+b)(1+(3h)/(10+\sqrt(4-3h)))`, avec `h = ((a-b)^2)/((a+b)^2)`
Cette formule donne le périmètre avec souvent plus d'une dizaine de chiffres exacts.
