Rechercher un sujet parmi les questions (en entrant un mot clé):
Sphère et plan en coupe
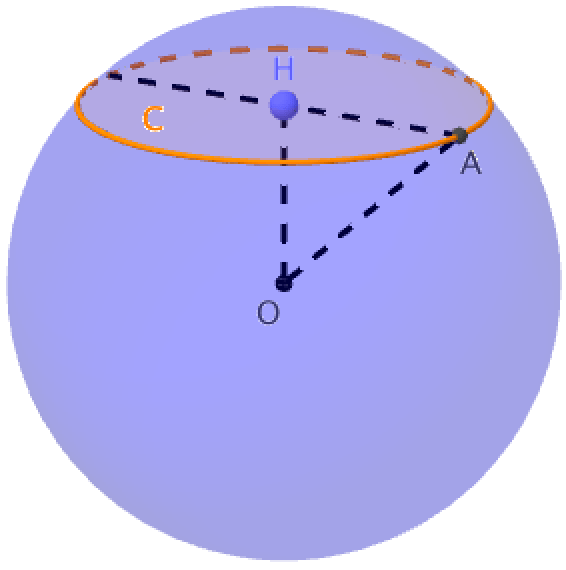
Considérons une sphère de centre O, un plan ne passant pas par le centre O coupe la surface sphérique selon une ligne dont tous les points sont à la même distance R du centre O de la sphère. Ces points sont à la même distance du pied de la perpendiculaire menée du centre O de la sphère au plan P : Le plan coupe la sphère selon un cercle (C) dont H est le centre et r le rayon ici HA.
Nous pouvons calculer le rayon r si on connait le rayon R et la distance OH. Nous continuerons par la surface de la calotte sphérique et son volume.
Publié le 14/02/2013 à 21:20:55 - Auteur :
REPONSES :
En appliquant la propriété de Pythagore au triangle OHA rectangle en H, nous obtenons :
r = √(R² - OH²) en nommant d la distance OH on a : r = √(R² - d²)
En nommant h la hauteur de la calotte (R = d + h ), on obtient aussi : r² = R² - (R-h)² = 2Rh - h²
La surface sphérique de la calotte est égale à S = 2πRh.
Le volume de la calotte est égal à V = πh²(3R - h)÷3.
démonstration :
En suivant la même méthode que pour la démonstration du segment sphérique de la page suivante volume d'un segment sphérique il suffit d'effectuer la somme entre 0 et h, on obtient alors :
∫0hπ(2Rx - x²)dx = [π(Rx² - x³/3)]0h = π(Rh² - h³/3) = πh²(3R - h)÷3 ou encore
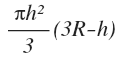
Réponse publiée le 15/02/2013 à 10:05:45 - Auteur : Webmaster
En remplaçant dans cette formule h par R, nous obtenons la formule d'une demi sphère et de là la formule de la sphère complète, que nous avons donc démontré facilement sans outils mathématiques trop importants.
Réponse publiée le 18/02/2013 à 11:36:01 - Auteur : Webmaster
Reste à démontrer la formule de surface sphérique de calotte, si je pouvais avoir de l'aide merci d'avance.
Réponse publiée le 18/02/2013 à 11:37:20 - Auteur : Webmaster
Bonjour, j'ai un exercice où un aquarium est considéré comme une calotte sphérique, il manque 4 cm pour avoir une sphère complète et on me demande de calculer la hauteur de l'aquarium h. Je sais pas si c'est important, mais le fond qui est aplati est négligé.
Réponse publiée le 14/03/2013 à 09:29:06 - Auteur : Charlotte
Si j'ai bien compris l'aquarium ressemble à ça :
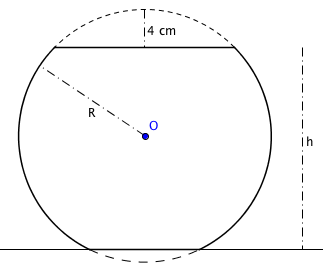
Dans ce cas il nous manque au moins une donnée celle du rayon R. Supposons que le rayon soit égal à 15 cm, alors nous pouvons déduire facilement la hauteur h = 30 − 4 = 26 cm et de là le volume de l'aquarium en négligeant le fond aplati :
V = 1/3×π×26²×(3×15 − 26 = 13450 cm³ soit en litres environ 13,4 L.
édit : 29/05/13 correction d'une erreur dans la valeur de h qui est égale à 26 et non 11; merci à Richard
Réponse publiée le 14/03/2013 à 09:50:31 - Auteur : Webmaster
L'aquarium plein a un volume de 14.137 L. La réponse ne semble pas cohérente.
Je pense que la hauteur demandée serait de 15+15−4 = 26 cm et avec 26 à la place de 11 on obtient 13450 cm3 soit 13.45 L de volume plein. Ce qui n'est pas demandé.
Réponse publiée le 25/09/2013 à 19:32:58 - Auteur : Richard
Tout à fait ! J'ai fait une belle erreur ! Je vais corriger.
Réponse publiée le 29/09/2013 à 16:12:11 - Auteur : Webmaster
bonjour,
simple commentaire pour correction :
dans la formule en fine de 3e ligne sous le shéma de la sphère :
r = R² - (R-h)² = 2Rh - h²
il s'agit de r² au lieu de r.
Réponse publiée le 12/03/2014 à 14:34:31 - Auteur : Michael
Tout à fait ! C'est corrigé merci bcp !
Réponse publiée le 12/03/2014 à 16:21:53 - Auteur : le Webmaster
L'aire de la surface d'une calotte est : 2π.r²(1-cosα) tq α est égale à l'angle entre les vecteurs HO et OA.
Réponse publiée le 18/11/2015 à 23:54:10 - Auteur : maryem
Tabranak c'est compliqué je suis en 3eme et ma prof nous a donner un exo comme celui la et j'y comprend r alors que je suis le meileur de ma class en maths ?
Réponse publiée le 01/10/2018 à 21:57:33 - Auteur : ATAMIKO
Alors enfin quelque chose qui te demande des efforts ! tu vas progresser !
Réponse publiée le 03/10/2018 à 07:59:57 - Auteur : Le webmaster
Vous êtes sûr que vous vous trompez pas sur l'Aire de la calotte de la sphère ?
Le Rayon ne devrait il pas être r est non pas R, le rayon du cercle qui coupe la sphère?
Réponse publiée le 02/09/2020 à 21:08:12 - Auteur : Matthew
Non, c'est bien R.
Réponse publiée le 11/10/2020 à 19:16:04 - Auteur : Le webmaster

