Rechercher un sujet (en entrant un mot clé):
Distance entre deux murs parallèles
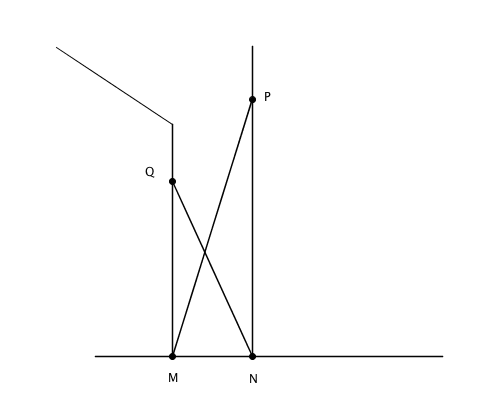
On se propose de trouver la distance séparant deux murs parallèles. Le bas d'une échelle de 7 mètres est positionné au pied du premier mur en M et s'appuie sur le second mur. De la même façon, le bas d'une échelle de 5 mètres est positionné au pied du second mur en N et s'appuie sur le premier mur. Ces deux échelles se croisent à 2 mètres du sol. Quelle est la distance entre les deux murs ?
Question publié : 05/03/2016 à 20:59:30 - auteur : j.quaspier
Par application du théorème de Thales, le problème se réduit à la résolution de l'équation
2(√(49-L²)+√(25-L²))=√(49-L²)√(25-L²), où L est la distance entre les murs (en mètre).
Cette équation peut être transformée en une équation du 4ème degré dont la solution recherchée est L=3.9548
réponse publiée : 15/03/2017 à 13:01:44 - auteur : F. Benamira
Effectivement !
réponse publiée : 17/03/2017 à 08:26:20 - auteur : Le webmaster
Peut-être est-il nécessaire d'expliciter un peu plus cette "équation du quatrième degré" :
Une élévation au carré sur l'équation donnée par F. Benamira donne :
4(49-L2 + 2√((49-L2)(25-L2)) + 25-L2) = (49-L2)(25-L2)
après une série de manipulations simples, on arrive à :
8√((49-L2)(25-L2) = (25-L2)(49-L2)-8(37-L2)
qui donne :
8√(1225 - 74L2 + L4) = (929 - 66L2 + L4)
Une deuxième élévation au carré donne ensuite :
64(1225 - 74L2 + L4) = (863041 - 122628L2 + 6214L4 - 132L6 + L8)
Un petit réarrangement final donne :
784641 - 117892L2 + 6150L4 - 132L6 + L8 = 0
Equation du huitième degré, mais où un changement de variable (x = L2) permet de se ramener à uné equation du quatrième degré.
Les deux solutions réelles exactes de cette équation sont absolument abominables, mais leur valeurs approchées sont faciles à obtenir (via la méthode de Newton-Raphson, notamment) :
x = 15.640196
x = 22.934893
Les deux autres solutions sont complexes conjuguées et ne sont donc pas intéressantes pour le problème. De plus, la solution x = 22.934893 conduit à une valeur de L = 4.789 m. Il s'agit d'une solution à rejeter car ne donnant pas la situation voulue (l'une des deux échelles est pratiquement couchée).
Ne reste que L = 3.954769 comme solution pour le problème.
réponse publiée : 25/07/2017 à 10:44:42 - auteur : Ashrod
