Rechercher un sujet (en entrant un mot clé):
Résoudre une équation de second degré
Comment résoudre une équation du second degré sans calculer de discriminant ? Comme le faisaient les Babyloniens.
Publié le 13/03/2013 à 09:57:57 - Auteur : Webmaster
Essayons de résoudre l'équation de second degré suivante : x² + 20x − 96 = 0
Nous pourrions utiliser la méthode du discriminant et nous aurions rapidement les solutions, mais comment pourrions nous faire sans calculer de discriminant ?
L'équation x² + 20x − 96 = 0 s'écrit aussi x² + 20x = 96
Imaginons la figure suivante :
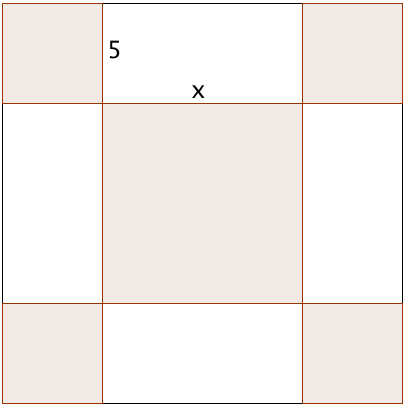
L'équation peut alors se traduit en terme de surface. En effet x² devient la surface du carré au centre de la figure et 20x représente la surface des 4 rectangles identiques de longueur x et largeur 5 (4 × 5x = 20x).
96 représente alors l'aire des surfaces du carré de coté x et des 4 rectangles.
Calculons l'aire de la surface du grand carré ? L'aire de la surface du grand carré est égale à la somme de 96 et des aires des 4 carrés de coté 5 soit : 96 + 4×5² = 196
Le grand carré a pour coté (x + 2×5) on obtient donc : (x + 10)² = 196
d'où x + 10 = 14 ou −(x + 10) = 14
x = 14 − 10 ou x = −14 − 10
x = 4 ou x = −24
Bien sûr au temps de Babylone seule la solution positive était prise en compte.
Vérification : (x − 4)(x + 24) = x² + 24x − 4x − 96 = x² + 20x − 96 nous retrouvons bien l'équation.
Réponse publiée le 13/03/2013 à 10:54:18 - Auteur : Webmaster
En utilisant la même méthode qui sera le premier à résoudre x² + 12x − 45 = 0
Réponse publiée le 13/03/2013 à 11:25:59 - Auteur : Webmaster
