Rechercher un sujet parmi les questions (en entrant un mot clé):
Fonction Bicarrée
Une fonction bicarrée est de la forme ax4 + bx² + c, avec a,b,c des réels et a non nul. Une fonction bicarrée est définie pour toutes les valeurs de x soit ]−∞;+∞[.
Pour tout x ∈ ]−∞;+∞[, ƒ(−x) = a(−x)4 + b(−x)² + c = ax4 + bx² + c = ƒ(−x) ; une fonction bicarrée est paire, il suffit donc de l'étudier sur [0;+∞[.
Etudions les variations f la fonction définie pour tout x ∈ ]−∞;+∞[ par ƒ(x) = 4x4 − 25x² + 36.
Publié le 25/02/2013 à 22:43:37 - Auteur : Webmaster
REPONSES :
ƒ est définie sur l'ensemble des réels, elle est continue et dérivable comme somme de fonctions continues et dérivables.
Pour tout x ∈ ]-∞;+∞[ par ƒ'(x) = 16x3 − 50x = 16x(x² − 50/16) et f' s'annule pour x = 0 et x = ± √50/4 ≈ 1.77 .
La courbe de la fonction f admet des tangentes horizontales où la dérivée de la fonction s'annule, donc pour x = 0 et x = ± √50/4.
16x > 0 pour x > 0 et (x² − 50/16) est de signe de −1 entre les racines.
| x¦−∞ | −√50/4 | 0 | +√50/4 | +∞¦ | ||||
| ƒ'(x)¦ | − | 0 | + | 0 | − | 0 | + | +∞¦ |
| ƒ(x)¦+∞ | décroit | m | croit | 36 | décroit | m | croit | +∞¦ |
La fonction ƒ admet un maximum en 0 égal à ƒ(0) = 36 et deux minima égaux (car la fonction est paire) en −√50/4 et √50/4 que nous pouvons calculer :
ƒ(−√50/4) = ƒ(√50/4) = 4(√50/4)4 − 25(√50/4)2 + 36 = 4(50/16)² − 25×(50/16) + 36 = (50/16)(50/4 − 25) + 36 = (50/16)(25/2 − 50/2) + 36 = (50/16)(−25/2) + 36 = −25²/16 + 36 = −3.0625.
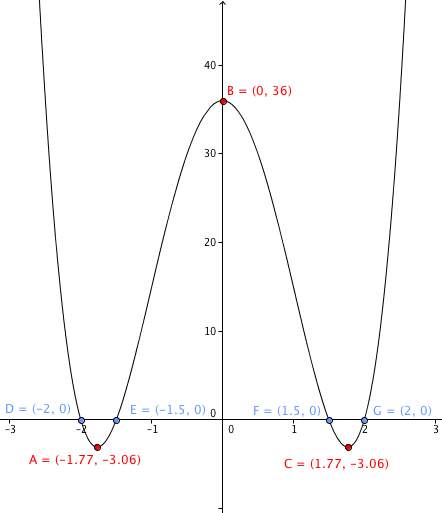
Nous obtenons les points A,B et C où la courbe de ƒ admet des tangentes horizontales. Les points A,B et C ont pour coordonnées respectifs (−√50/4,−3.0625),(0;36) et (√50/4;−3.0625) (en rouge sur le graphique)
Les minima étant négatifs, les variations de la fonction nous indiquent que la fonction s'annule 4 fois. Recherchons les racines de ƒ(x) = 0.
On pose X = x², ƒ(x) = 0 devient alors équivalent au système suivant :
¦ 4X² − 25X + 36 = 0 (1)
¦ X = x² (2)
Le discriminant du trinôme 4X² − 25X + 36 est égal à 625 − 576 = 49 > 0 , l'équation 4X² - 25X + 36 = 0 admet deux solutions réelles et distinctes :
Les racines de l'équation (2) deviennent :
La courbe de la fonction ƒ coupe donc l'axe des abscisses aux point D = (−2;0) , E = (−3/2;0) , F = (3/2;0) et G = (2;0) (en bleu sur le graphique)
Graphe de la fonction étudiée :
Réponse publiée le 25/02/2013 à 23:04:50 - Auteur : Webmaster
Deuxième exemple numérique : étudions la fonction bicarrée définie par g(x) = −x4 − 2x² + 1.
g est définie sur l'ensemble des rééls, elle est continue et dérivable comme somme de fonctions continues et dérivables. La fonction g, comme toute les fonctions bicarrées, est paire.
Pour tout x ∈ ]-∞;+∞[ par g'(x) = −4x3 − 4x = −4x(x² + 1).
g' s'annule seulement pour x = 0 car (x² + 1) > 0 pour tout x.
Pour tout x <0 , g'(x) est strictement positif et pour tout x < 0 , g'(x) est strictement négatif.
La fonction g est donc strictement croissante sur ]−∞;0[ et strictement décroissante sur ]0;+∞[.
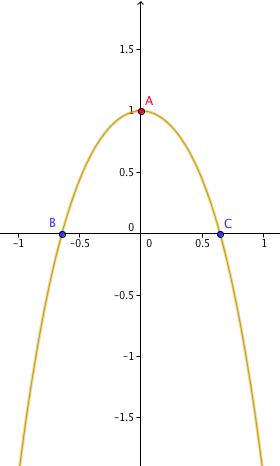
Comme g' s'annule en 0, la fonction g passe par un maximum égal à g(0) = 1 qui correspond au point A = (0;1) sur le graphe.
La courbe de g a une forme parabolique et admet l'axe des y comme axe de symétrie ( conséquence que g soit paire ). Elle coupe donc l'axe des abscisses en 2 points B et C d'ordonnée 0 et d'abscisse les solutions de l'équation g(x) = 0.
g(x) = 0 ⇔ −x4 − 2x² + 1 (1)
On pose X = x², g(x) = 0 devient alors équivalent au système suivant :
¦ −X² − 2X + 1 = 0 (2)
¦ X = x²
Le discriminant de −X² − 2X + 1 est égal à : 4 + 4 = 8 est strictement positif donc (2) admet deux solutions réelles X = (2 ± √8)/(−2) = −(1 ± √2)
Seules les solutions où X > 0 sont envisageables, il reste donc X = −(1 − √2) = √2 − 1.
Les solutions de (1) sont celles de : x² = √2 − 1 donc x = ±√(√2 − 1) ≈ ±0.64
Les coordonnées de B et C sont respectivement (−√(√2 − 1);0) et (√(√2 − 1);0)
Soit le graphe de la courbe parabolique :
Réponse publiée le 26/02/2013 à 15:49:11 - Auteur : Webmaster

