Rechercher un sujet parmi les questions (en entrant un mot clé):
Le crocodile et le zèbre (pb de math)
Je vous présente un problème qui a été donné aux lycéens écossais pour leur examen de fin de secondaire. Apparemment cette question leur a posé beaucoup de soucis et traumatisé un bon nombre d'entre eux. A tel point qu'une pétition a été lancé sur le net et le nombre de point pour obtenir l'examen réduit !
Il s'agit d'un problème d'étude de fonction et même si la présentation est originale (quoique, j'ai déjà vu ce problème sous d'autres formes) sa résolution n'est pas inaccessible pour un élève de seconde.
Je vous laisse lire le sujet en anglais of course.
Publié le 15/10/2015 à 09:56:20 - Auteur : Le webmaster

REPONSES :
Il s'agit d'étudier le temps que met un crocodile à atteindre sa proie (le zèbre) sachant que le zèbre est sur l'autre rive d'une rivière et a une distance 20 m. Le crocodile ne se déplaçant pas à la même vitesse dans l'eau que sur la terre ferme, j'ai d'abord pensé qu'il fallait déterminer la fonction vitesse mais non celle-ci est donnée.
Cette fonction T donne le temps en seconde en fonction de x en mètre; elle est égale à :
T(x) = 5√(36+X²) + 4(20-X)
Cette fonction donne en fonction de la distance x en mètres le temps que mettra le crocodile à atteindre le zèbre.
La distance x peut varier de 0, si le crocodile décide de traverser perpendiculairement la rivière, à 20 si le crocodile décide d'atteindre sa proie en en nageant en ligne droite.
les questions correspondent à :
a) (I) à la valeur de T(X) pour X = 0
a) (II) à la valeur de T(X) pour X = 20
(b) le temps minimum correspondra au minimum de la fonction T que l'on pourra trouver avec une calculatrice graphique
Bref, pas de dérivée à calculer et de tableau de variation à dresser.
Réponse publiée le 15/10/2015 à 10:48:04 - Auteur : Le webmaster
Comment on peut résoudre ce problème avec une simple TI 82
Dans f(x) (touche : [ƒ(x)]) il faut entrer la fonction T, il faut entrer dans Y1 exactement la ligne suivante :
5√(36+X²)+4(20−X)
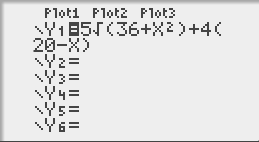
Ensuite dans définition table (touches : [2nde]+[déf table]), nous voulons les valeurs pour x de 0 à 20, il faut entrer les valeurs suivantes :
DébTable = 0 (version english TblStart)
PasTable = 5 (version english Tbl)
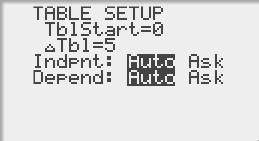
Le PasTable égal à 5 nous assure d'obtenir la valeur pour x = 20.
Il suffit ensuite d'aller dans table (touches : [2nde]+[table]) pour obtenir toutes les valeurs à partir de x = 0, x = 5, x = 10, x = 15 et x = 20. Cette méthode évite des erreurs de calculs si l'on calculer à la machine 5√(36+20²)+4(20−20) les élèves se trompent souvent par exemple dans l'ordre des parenthèses.
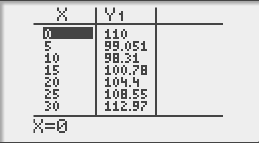
Nous avons donc les 2 valeurs qui nous intéressent :
- T(20) = 104,4 secondes; réponse de la question a) i)
- et T(0) = 110 secondes; réponse de la question a) ii)
Pour la question b) il est juste demandé de relever le minimum de la fonction entre 0 et 20 grâce à une calculatrice graphique, la TI-82 fait cela parfaitement.
Pour cela il faut configurer la fenêtre (touche : [fenêtre]) dans laquelle la courbe de la fonction sera tracée comme ci dessous :
Pour Xmin 0 et Xmax 20.
Pour Ymin 95 (parce que je connait la réponse, mais on peut faire un essais à 60 et ensuite recentre la fenêtre afin d'avoir une meilleure valeur du minimum).
Pour Ymax 110 c'est le plus long parcourt.
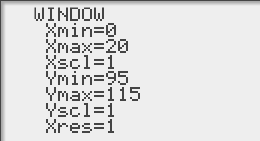
Ensuite il suffit de tracer la courbe de la fonction T (touche : [trace]) et de se balader tout le long jusqu'à atteindre le minimum.
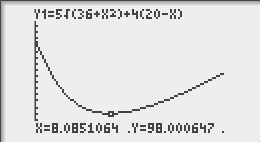
Nous relevons comme valeur minimum x = 8,08 m et donc 98 secondes.
Même si de nos jours c'est souvent comme cela que les choses sont demandées aux lycéens (du moins aux élèves de seconde), ce n'est que très approximatif. Je vous donnerai une méthode plus rigoureuse prochainement.
Réponse publiée le 16/10/2015 à 12:20:46 - Auteur : Le webmaster
Méthode plus rigoureuse !
Pour la question a) rien ne change, mais pour la question b) il faut étudier la fonction T entre 0 et 20.
T est une fonction définie et dérivable (comme composition de fct dérivables) sur l'intervalle [0;20].
T(X) = 5√(36+X²) + 4(20−X) = 5(36+X²)½ + 4(20−X)
T'(X) = 5(½×2X×(36+X²)½−1) + 4(-1)
T'(X) = 5X×(36+X²)-½ − 4
T'(X) = 5X/(36+X²)½ − 4
ou encore
T'(X) = 5X/√(36+X²) − 4
ou encore en mettant le tout au même dénominateur
T'(X) = (5X−4√(36+X²))/√(36+X²)
en résumé :
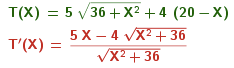
il faut étudier le signe et les zéros de T' en effet les extremums de T sont atteints lorsque T' s'annule en changeant de signe.
T'(X) = (5X−4√(36+X²))/√(36+X²) ≥ 0
⇔ 5X−4√(36+X²) ≥ 0 car √(36+X²) > 0 pour tout X
⇔ 5X ≥ 4√(36+X²)
⇔ 25X² ≥ 4²(36+X²) car 5X ≥ 4√(36+X²) > 0
⇔ 25X² ≥ 576 + 16X²
⇔ 25X² − 16X² ≥ 576
⇔ 9X² ≥ 576
⇔ X² ≥ 576÷9
⇔ X² ≥ 64
⇔ X ≥ 8 car X ∈ [0;20]
Donc T'(X) ≥ 0 pour tout X ∈ [8;20] et T'(X) ≤ 0 pour tout X ∈ [0;8]
Donc la fonction T' s'annule en X = 8 en changeant de signe négative puis positive, donc T admet bien un unique minimum en X = 8 pour X compris entre 0 et 20.
T(8) = 5√(36+8²) + 4(20−8) = 5√100 + 48 = 50 + 48 = 98
Le plus court chemin du crocodile est lorsque X = 8 et il mettra 98s pour atteindre sa cible.
Réponse publiée le 17/10/2015 à 12:50:45 - Auteur : Le webmaster

