Rechercher un sujet parmi les questions (en entrant un mot clé):
Calculer l'aire des Lunules d'Hippocrate
Soit un triangle ABC rectangle en A avec K milieu du segment [CB], I au milieu du segment [AC] et J au milieu du segment [AB].
Traçons les demi-cercles de centre K et de diamètre [BC], de centre I de diamètre [AB] et de de centre J et de diamètre [AC].
Les deux surfaces en forme de croissants délimités par les demi-cercles sont appelées les Lunules d'Hipocrate. Calculons leurs surfaces.
Publié le 24/02/2013 à 14:12:10 - Auteur : Webmaster
REPONSES :
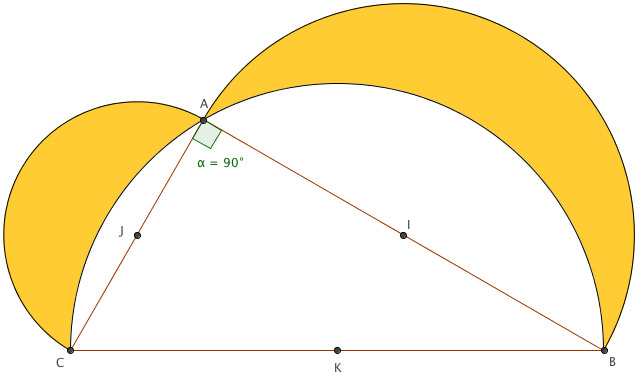
Pour calculer l'aire de la surface des 2 lunules (en jaune), il suffit :
aux aires S1 et S2 des 2 demi disque de diamètres [AC] et [AB] et à l'aire SABC du triangle ABC,
de soustraire l'aire S3 du demi disque de diamètre [BC].
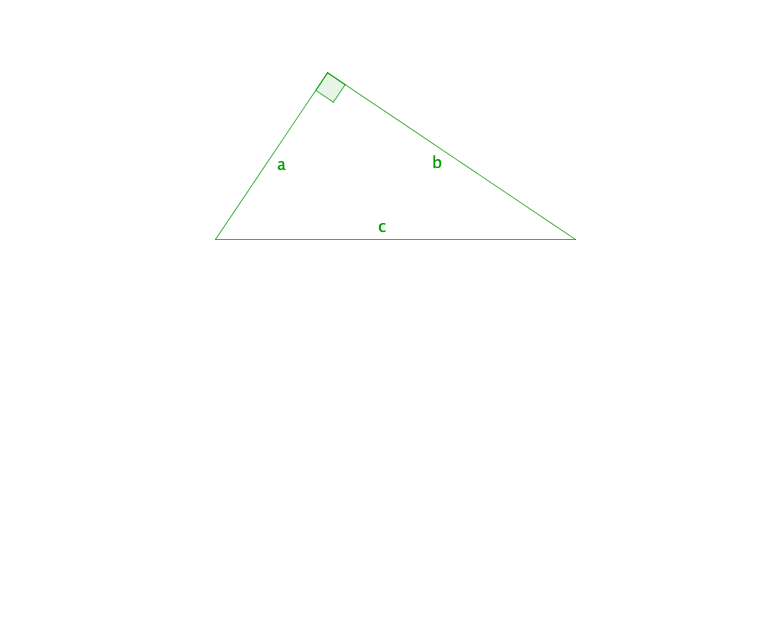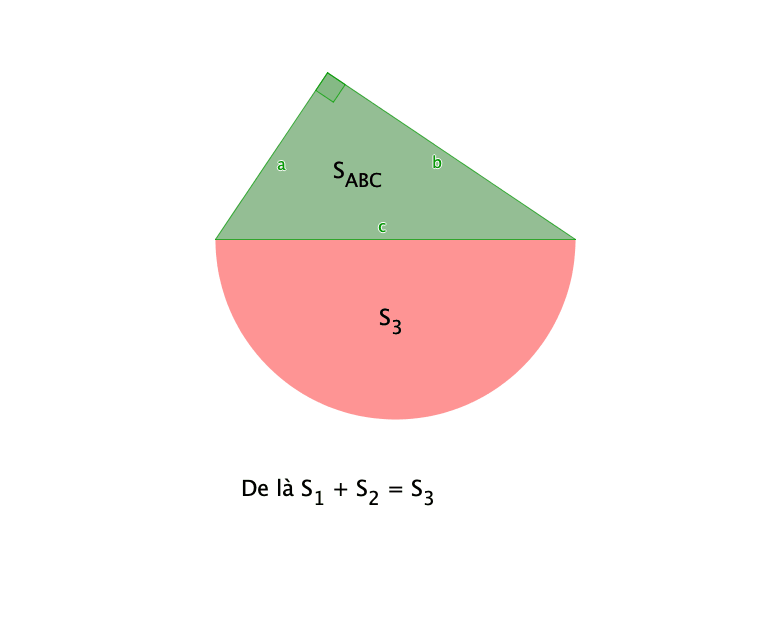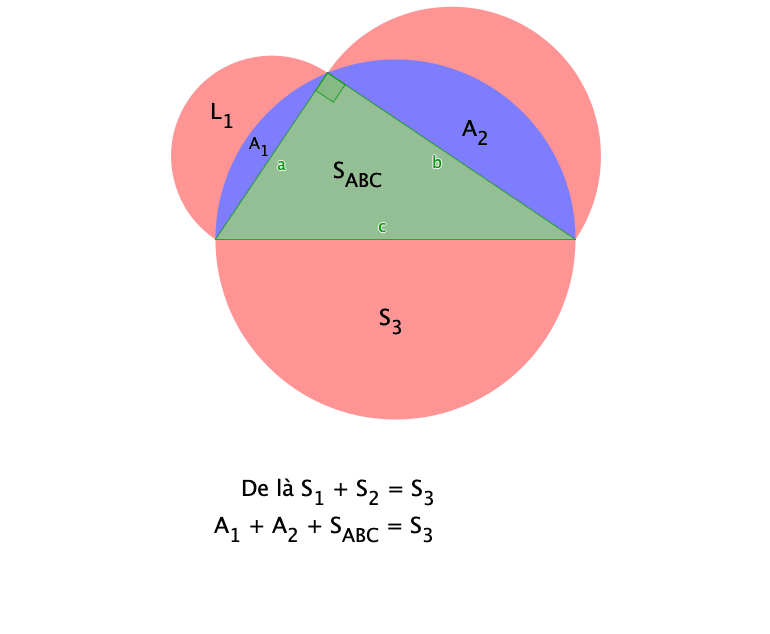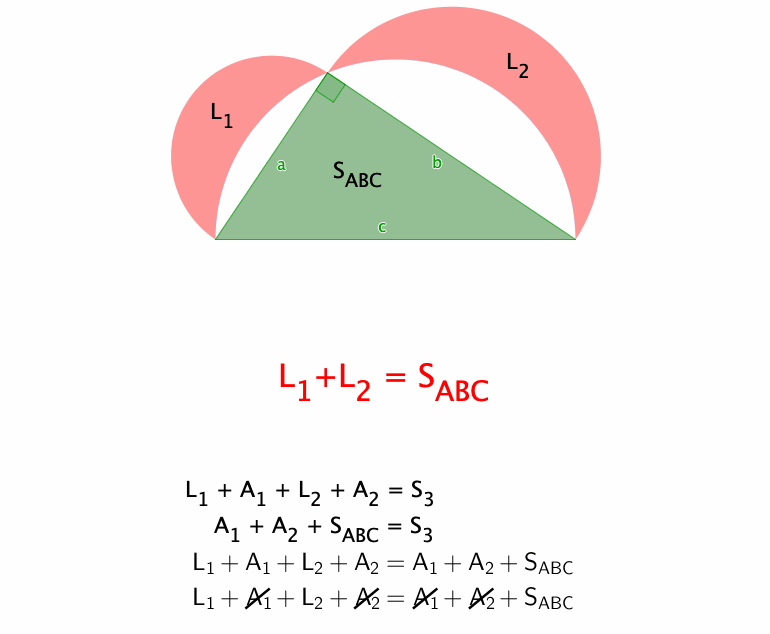
L'aire des 2 lunules est égale à : S1 + S2 + SABC − S3 notons (1) cette relation.
En nommant respectivement a, b, c les mesures des segments [AC], [AB] et [BC] on obtient :
`S_1 =1/2π(a/2)^2 = {πa^2}/8`;
`S_2 = 1/2π(b/2)^2 = {πb^2}/8`;
et `S_3 = 1/2π(c/2)^2 = {πc^2}/8`
L'aire de la surface `S_{ABC} = {a × b} / 2 = 1/2ab`
La propriété de Pythagore nous donne :
`a^2 + b^2 = c^2`
En multipliant par π/8 chaque membre de cette relation on obtient
`π/8×(a^2 + b^2) = π/8×c^2`
`π/8a^2 + π/8b^2 = π/8c^2`
On reconnaît : S1 + S2 = S3 notons (2) cette relation.
El alors la relation(1) (qui est égale à l'aire des lunules) devient (en utilisant la relation (2)) :
L'aire de la surface des deux lunules est donc égale à l'aire de la surface du triangle ABC.
Un petit gif pour illustrer tout ça :
Réponse publiée le 24/02/2013 à 20:33:32 - Auteur : Webmaster
il n'y aurait pas une façon beaucoup plus simple de calculer ?
Réponse publiée le 11/09/2013 à 15:32:58 - Auteur : anonyme
Je n'ai absolument rien compris avec ces histoires de Sabc... :(
Réponse publiée le 16/02/2014 à 15:11:59 - Auteur :
S O S je comprends pas c dur ....
Réponse publiée le 14/01/2015 à 17:58:23 - Auteur :
Tout de même pas si dur que cela :
fixons un peu les idées :
S1 représente la surface du demi disque de diamètre [AC]
S2 représente la surface du demi disque de diamètre [AB]
S3 représente la surface du demi disque de diamètre [BC]
A partir de la propriété de Pythagore on démontre la relation :
S1 + S2 = S3
L'aire des lunules en jaune quand à elle est égale à :
L'aire du triangle + l'aire des deux demi-disque de diamètre [AC] et [AB] à laquelle on retira l'aire du grand demi disque de diamètre [BC]
cela se traduit par (en nommant SABC l'aire du triangle ABC) :
Aire en jaune = S1 + S2 + SABC − S3 = SABC
L'aire en jaune est égale à l'aire du triangle ABC.
Réponse publiée le 17/01/2015 à 12:07:05 - Auteur : Webmaster
C'est compliqué a comprendre il n'y a pas un théorème ou une propriété plus facile à mettre un oeuvre et à expliquer.
Réponse publiée le 08/03/2015 à 17:58:53 - Auteur : pipolaki6438
Hélas non :/
Réponse publiée le 08/03/2015 à 21:51:24 - Auteur : Le webmaster
Bonjour, est ce que l'aire des lunules peut être 8² quand l'aire du triangle est 8cm² ?
Réponse publiée le 17/11/2016 à 10:31:45 - Auteur : Justine
L'aire des lunules est toujours égale à l'aire du triangle ! Donc oui.
Réponse publiée le 19/11/2016 à 08:33:45 - Auteur : Le webmaster
J'ai le même exercice en ce moment... Horrible
Réponse publiée le 01/03/2017 à 14:54:38 - Auteur : Un Terrien
Mais non je le répète "L'aire des lunules est toujours égale à l'aire du triangle".
Réponse publiée le 05/03/2017 à 14:56:49 - Auteur : Webmaster
Bonjour excusez moi mais dans mon cas on me demande de déduire que la somme des aires des lunules est égale à l'aire du demi cercle de diamètre BC ... Comment dois je procéder ??
Réponse publiée le 04/11/2018 à 15:06:08 - Auteur : Une alicorne
Cette question n'est pas si mauvaise ... J'ai un prof qui me demande la même chose ... Mais le truc c'est que c'est pour demain ... Donc aidez moi svp
Réponse publiée le 04/11/2018 à 15:14:06 - Auteur : Le BG
Vous avez dû mal comprendre l'énoncé c'est :
- La somme des aires des demi-disques de diamètre [AC] et [AB] qui est égale à l'aire du demi-disque de diamètre [BC].
C'est démontré plus haut sous la forme : S1+ S2 = S3
C'est une évidence le triangle est rectangle en A et la relation de Pythagore nous dit que :
AC2 + AB2 = BC2
il suffit ensuite de multiplier par ½π pour obtenir les surfaces voulues :
½π.AC2 + ½π.AB2 = ½π.BC2
S1+ S2 = S3
Réponse publiée le 04/11/2018 à 21:56:28 - Auteur : Le webmaster
Dans l'expression : ½π.(b/2)² = π.b²/8 pourquoi 8 ?
Réponse publiée le 15/11/2018 à 18:40:14 - Auteur : Mat
Voilà le produit de ½ par le carré de b/2 donne :
½ × b²/2² = ½ × b²/4 = b²/(2×4) = b²/8
Réponse publiée le 16/11/2018 à 07:13:57 - Auteur : Le webmaster
C'est bien beau de prouver que S1 + S2 = S3 mais comment fait-on pour trouver que les deux lunules sont égales à l'aire du triangle ?
Réponse publiée le 16/01/2019 à 06:54:37 - Auteur : Un mec perdu
Trop compliqué
Réponse publiée le 02/02/2019 à 22:08:16 - Auteur : C'est mon devoir
Je vois que ce n'est pas compris par tous. je vais modifier cette page afin que ce soit plus simple.
Réponse publiée le 05/02/2019 à 13:50:21 - Auteur : Le webmaster
Mais je crois qu'il y a une erreur dans l'exercice ou alors il faut m'expliquer, quand vous marquer que `S1 = π times a^2/8` , je ne comprend pas parce que `π times a²` c'est pas le rayon du cercle c'est le diamètre.
Réponse publiée le 25/10/2019 à 14:57:51 - Auteur : Cici
`a` représente bien le diamètre. Et `S_1` le demi-disque, d'où :
`S_1 = 1/2 times pi (a/2)^2`
Réponse publiée le 27/10/2019 à 17:52:11 - Auteur : Le webmaster

