Rechercher un sujet (en entrant un mot clé):
Géométrie sur quadrillage
Problème : Sur un quadrillage on trace un rectangle dont les sommets sont des nœuds du quadrillage et les côtés suivent le quadrillage. On trace une des diagonales de ce rectangle et on numérote les points d’intersection de sa diagonale avec les lignes du quadrillage en commençant à 0.
Trouver une formule qui donne le nombre obtenu sur le sommet opposé à celui de départ à l’aide des dimensions a et b du rectangle on attribue la valeur 0 au premier point d'intersection.
Publié le 04/10/2013 à 15:40:31 - Auteur : Gaëtan
a et b sont des entiers car le rectangle suit le quadrillage.
Si a = 1 ou b = 1 quelque soit la valeur du second, la diagonale ne passe par aucun noeud.
Supposons 1 < a < b, il y a toujours au plus (a-1) noeud(s).
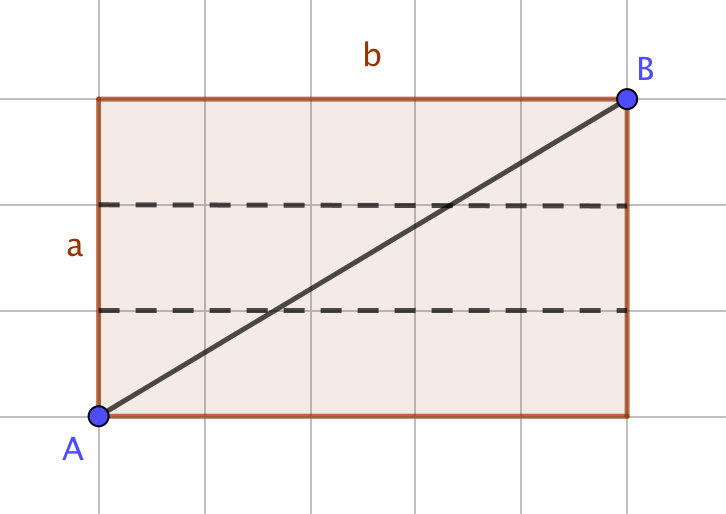
Si a divise b alors il y a (a−1) noeud(s) sinon il n'y a pas de noeud.
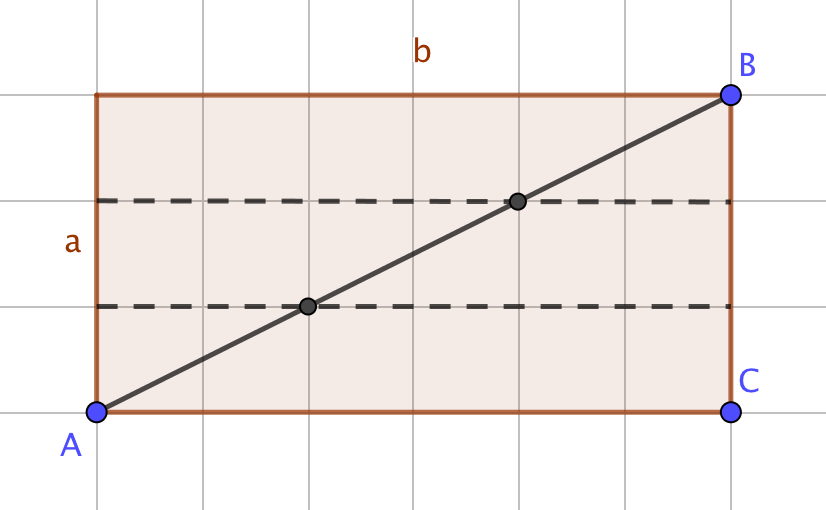
Réponse publiée le 21/10/2018 à 17:07:51 - Auteur : Le webmaster
Exemple : avec a = 5 et b = 10 ⇒ 4 noeuds.
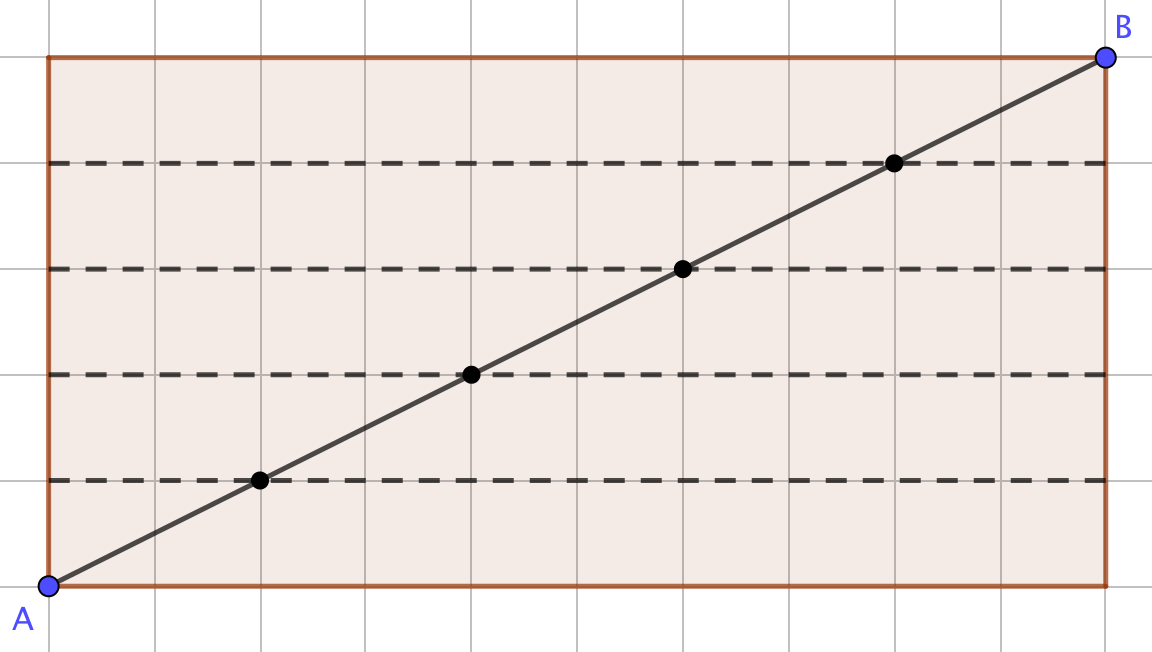
Réponse publiée le 21/10/2018 à 17:23:31 - Auteur : Le webmaster
