Calculis

Rechercher un sujet (en entrant un mot clé):

Voici 2 figures qui vont nous aider.

On a tracé ici le segment [AB], le milieu H du segment [AB]. On construit la droite D perpendiculaire à la droite (AB) en H. Cette droite coupe l'arc (AB en F et le centre de l'arc appartient à cette droite.



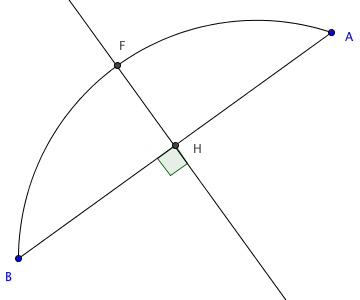
Par hypothèse nous connaissons la longueur HF de la figure ci-dessus.

On peut facilement par une construction géométrique trouver le centre du cercle qui porte l'arc (AB. Par exemple en construisant la médiatrice du segment [FA]. Le point d'intersection de la droite D et de cette médiatrice est le centre recherché.



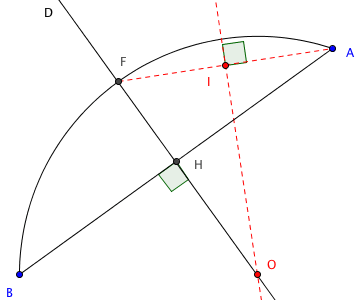
Quelle est la valeur du rayon ?

Si on connait la longueur du segment [AB]. On peut calculer facilement le rayon.

Soit c la longueur du segment [AB], r le rayon et f la flèche (la longueur FH) alors on la relation suivante dans le triangle rectangle AHO :

(OA)² = (c/2)² + (HO)²

or OA = r et HO = r−f

r² = c²/4 + (r−f)²

et de là on peut calculer r.

Si on ne connait pas la longueur du segment [AB], cela me semble impossible. Il nous faut la longueur de la corde c. Connaitre la longueur de l'arc sans connaitre le rayon ne nous permet pas de calculer c.

Réponse publiée le 08/05/2016 à 20:27:41 - Auteur : Le webmaster

donc pour finir r= c²/(8f) + f/2
(si je ne me trompe...)

Réponse publiée le 02/06/2017 à 08:54:27 - Auteur : moi

On peut développer un peu plus effectivement :

r² = c²/4 + (r−f)²

r² = c²/4 + r² − 2rf + f²

2rf = c²/4 + f²

r = (c²/4 + f²) / 2f

r = c²/(8f) + f/2

suite à la remarque de JPL en posant a = f et b = c/2 on peut obtenir une formule plus sympathique :

r = (c/2)²/(2f) + f/2

r = (c/2)²/(2f) + f²/2f

r = b²/2a + a²/2a

r = (a² + b²)/2a

Réponse publiée le 17/07/2017 à 10:48:00 - Auteur : Webmaster

très satisfait de la solution.

encore merci.

Réponse publiée le 10/04/2018 à 15:34:18 - Auteur : RD

On peut aussi aboutir à ceci : r = (f²+BH²)/ 2f
en utilisant des variables a et b ça donne une formule presque facile à retenir ! (a²+b²)/2a

Réponse publiée le 27/02/2019 à 16:21:18 - Auteur : JPL

Merci. je cherchais cette methode

Réponse publiée le 09/03/2019 à 23:19:59 - Auteur : steeves

Bonne remarque de la part de JPL, effectivement cela donne une formule facile à retenir ;).

Réponse publiée le 15/03/2019 à 09:35:38 - Auteur : Le webmaster

Merci.

Réponse publiée le 05/04/2019 à 06:42:38 - Auteur :

Merci beaucoup pour cette méthode qui m'a permis de calculer le rayon à utiliser pour faire un arc de cercle sur une tête de lit. (largeur 160 cm et 12 cm de flèche, soit un rayon de 272 cm).

Par contre pour info, dans Excel, j'ai du rajouter des parenthèses autour de 2a pour que le résultat soit juste. cela donne donc :

r = (a² + b²)/(2 x a)

Merci encore.

Réponse publiée le 19/08/2019 à 09:50:22 - Auteur : Laurent 07

haha effectivement, votre remarque ressemble beaucoup à la question de math de cet été sur les réseaux : 8÷2(2+2)

Réponse publiée le 19/08/2019 à 10:38:30 - Auteur : Le webmaster

La longueur de mon arc mesure 15450mm la flèche mesure 88mm. puis-je connaitre le rayon ?

Réponse publiée le 24/02/2020 à 14:28:56 - Auteur : pumba44

Environ 339075 mm

Réponse publiée le 28/02/2020 à 14:08:46 - Auteur : Le webmaster

Bonjour,
Comment calculez vous la taille de la flèche ? (Désolée je n'en suis pas une de toute évidence...)
Bonne soirée

Réponse publiée le 30/03/2020 à 20:23:21 - Auteur : Léa

Très intéressant... mais ne répond pas vraiment à la question initiale. En effet, les données d'entrée sont flèche et arc et non flèche et corde.

Je repose donc la question, connaissez-vous une méthode pour calculer le rayon d'un cercle à partir de la longueur de l'arc et de la flèche?

Réponse publiée le 11/03/2021 à 12:25:12 - Auteur :

À l'époque lorsque j'ai cherché c'était pour moi impossible. je le dit dans le premier post.

Réponse publiée le 13/03/2021 à 15:37:20 - Auteur : Le webmaster