Rechercher un sujet parmi les questions (en entrant un mot clé):
Comment la calculer la surface d'une rosace ?
Comment calculer l'aire de la surface des rosaces suivantes :
- une rosace à quatre pétales contenue dans un carré de coté de longueur 2c
- la rosace de notre enfance à six pétales à partir de cercles de même rayon R
Publié le 01/03/2013 à 11:29:26 - Auteur : Webmaster
REPONSES :
On construit un rosace à 4 branches inscrit dans un carré de coté dont la longueur est égal à 2c. Nous obtenons la figure suivante :
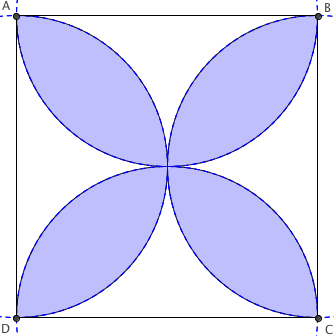
On se propose de calculer la surface bleue de la rosace. Il s'agit de 4 fois la même intersection de disque de rayon R.
R est égal à la moitié du coté du carré d'où R = c.
La formule de la surface d'une intersection de disque est détaillée à cette page : http://calculis.net/comment/aire-intersection-disques-35.
Soit S l'aire de la surface d'une branche alors :
S = 2R²cos−1( d / 2R ) − ½d√( 4R² − d² ) où d est la distance des deux rayons des disques.
d est la diagonale d'un carré de coté c d'où d = √2c et d² = 2c²
S devient alors en fonction de la mesure c :
S = 2c²cos−1( √2/2 ) − ½√2c√( 4c² − 2c² ) or cos(π/4) = √2/2
S = 2c² × π/4 − ½√2c√( 2c² )
S = c² × π/2 − ½√2c√2c
S = c² × π/2 − ½2c²
S = c² × π/2 − c² = c²(π/2 − 1)
L'aire totale de la rosace est égale à : 4 × S = 4c²(π/2 − 1) = c²(2π − 4).
Réponse publiée le 03/03/2013 à 15:58:56 - Auteur : Webmaster
Nous pouvons obtenir le résultat précédent sans utiliser la formule d'intersection de disque. Plus simplement à la surface d'un carré de coté c nous pouvons soustraire le quart de cercle de rayon c notons S' cette surface, alors la surface de la rosace est égale à : (2c)² − 8 × S'.
S' = c² - πc²/4 = c²(1 − π/4) (surface d'un quart de disque πr²/4)
alors (2c)² − 8 × S' = 4c² − 8c²(1 − π/4) = c²(4 − 8 + 2π) = c²(2π − 4)
Cette démonstration est nettement plus accessible.
Réponse publiée le 04/03/2013 à 11:13:54 - Auteur : Webmaster
Voici une rosace à 6 branches inscrit dans un cercle de rayon R. C'est la rosace que tout le monde connait trés simple à réaliser avec un compas.
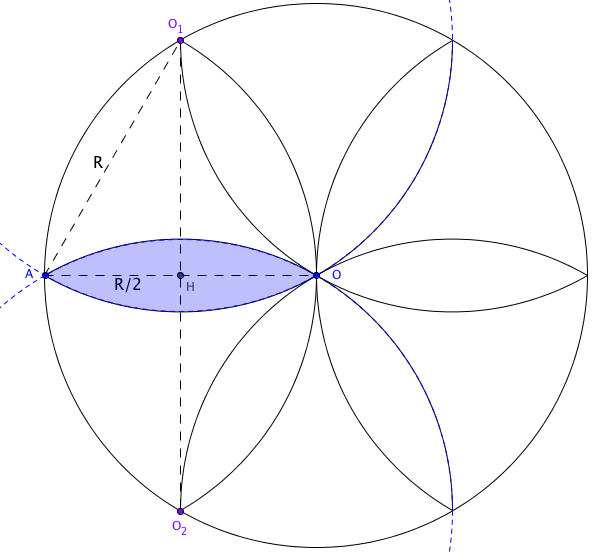
Si l'on souhaite utiliser la formule de l'aire de la surface de l'intersection de deux disques, il faudra connaitre la distance O1O2 distance des deux centres des disques.
Il suffit d'appliquer la propriété de Pythagore dans le triangle HAO1 et l'on obtient : d = √3R
Ensuite remplacer dans la formule 2R²cos−1( d / 2R ) − ½d√( 4R² − d² ) et l'on obtient :
2R²cos−1( √3R / 2R ) − ½√3R√( 4R² − (√3R)² )
= 2R²cos−1( √3/2 ) − ½√3R√( 4R² − 3R² ) or cos(π/6) = √3/2
= 2R²π/6 − ½√3R.R
= R²π/3 − R²√3/2
= R²(π/3 − √3/2)
La surface totale de la rosace est égale à : 6R²(π/3 − √3/2).
On peut aussi utiliser la formule de l'aire d'un segment de disque. Le segment de disque à considérer et celui dont la corde est R et l'angle dont il est issu π/3 (il s'agit d'un triangle équilatéral) l'aire totale sera égale à 12 fois l'aire du segment.
l'aire du segment est égal à ½ R² ( α − sin α ) avec α en radian soit :
½ R² ( π/3 − sin(π/3) ) or sin(π/3) = √3/2 d'où ½ R² ( π/3 − sin(π/3) ) = ½ R² ( π/3 − √3/2 )
La surface totale de la rosace est égale à : 12 × ½ R² ( π/3 − √3/2 ) = 6R² ( π/3 − √3/2 ) on retrouve bien le résultat précédent.
Réponse publiée le 04/03/2013 à 11:16:40 - Auteur : Webmaster
Mais comment fait-on pour calculer le périmètre alors ? Moi pour mon exercice, il faut calculer une rosace à 4 pétales aussi mais dans un carré de 10 cm de côté.
Réponse publiée le 08/03/2013 à 11:07:07 - Auteur : Camila974
Bonjour, Camila974 alors si c'est exactement le même forme de rosace que dans le premier exemple avec un carré de 10 cm alors il suffit de remplacer c par 5 dans la formule obtenue puisque c'était pour un carré de coté 2c.
Ce qui donne : c²(2π − 4) = 5²(2π − 4) = 25(2π − 4) ≈ 57 cm² avec π = 3,14
Ok je me suis emballé, il s'agit du périmètre ! La rosace dans un carré du premier exemple est délimitée par 2 cercles (4 demi-cercles) de même rayon égal à la moitié d'un coté du carré, soit 5 cm dans ton cas.
Le périmètre (plutôt la circonférence) d'un cercle de rayon R est égal à 2πR soit dans ton cas 2×5×3,14 = 31,4 cm et pour les deux cercles : 2 × 31,4 = 62,8 cm.
j'espère t'avoir aidé.
Réponse publiée le 08/03/2013 à 11:55:28 - Auteur : Webamster
peut-on calculer la partie bleu de la rosace sans utiliser s' ?
Réponse publiée le 14/03/2014 à 15:11:03 - Auteur : anonyme
dans mon énoncé le coté du carré est égal à 2cm et les rayons des cercles mesurent 1cm, dans ca cas comment je peux faire ?
Réponse publiée le 14/03/2014 à 15:26:14 - Auteur : anonyme
merci les cools trop facile la rosacea!!!
Réponse publiée le 23/07/2014 à 17:16:41 - Auteur : jj

