Rechercher un sujet (en entrant un mot clé):
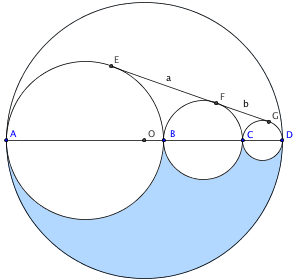
Quel est l'aire de la surface bleue ?
Démontrer que la surface en bleue est égale à :
Publié le 17/01/2015 à 14:13:43 - Auteur : Webmaster
Préalable: le fait que les 3 cercles soient ainsi disposés (tangents extérieurement) implique que l'homothétie positive qui transforme C1 (le plus grand cercle) en C2 (le cercle "moyen") et aussi celle qui transforme C2 en C3 (le petit cercle).
Il en résulte que, r1, r2, r3 étant les rayons respectifs de ces cercles :
r2/r1 = r3/r2 donc r2 = √(r1r3) [égalité1].
O1, O2, O3 étant les centres respectifs de C1, C2, C3, traçons les segments [O1E], [O2F], [O3G] tous perpendiculaires à la tangente commune.
Traçons la parallèle à (AD) passant par F : elle coupe[O1E] en K, puis la parallèle à (AD) passant par G : elle coupe [O2F] en L.
On peut dire que : KF = O1O2 = r1 + r2 (car KFO2O1 est un parallélogramme).
De même : LG = r2 + r3.
Alors, dans les triangles rectangles KEF et GFL : EF² = KF² − KE² et FG² = LG² − LF²
soit :
a² = (r1+r2)² − (r1 − r2)² = 4r1r2 et b² = (r2 + r3)² − (r2 − r3)² = 4r2r3.
D'où : a² + b² + ab = 4r1r2 + 4r2r3 + 4√(r1r2²r3) = 4r1r2 + 4r2r3 + 4r1r3 (d'après l'égalité 1).
Il s'en suit : a² + b² + ab = 4(r1r2 + r2r3 + r1r3) [égalité2].
Le cercle de diamètre AD a pour rayon r1+r2+r3,
d'où l'aire bleue : ½π[(r1 + r2 + r3)² − r1² − r2² − r3²] = ½π(2r1r2 + 2r2r3 + 2r3r1) = π(r1r2 + r2r3 + r1r3).
En rapprochant de l'égalité 2, on a bien : Sbleue = ¼π(a² + b² + ab)
Réponse publiée le 01/07/2015 à 07:32:27 - Auteur : PERRON
Merci pour votre participation ! Belle démonstration !
Réponse publiée le 01/07/2015 à 10:18:50 - Auteur : Le webmasteur
