Rechercher un sujet parmi les questions (en entrant un mot clé):
Calculer le volume d'une portion de tore
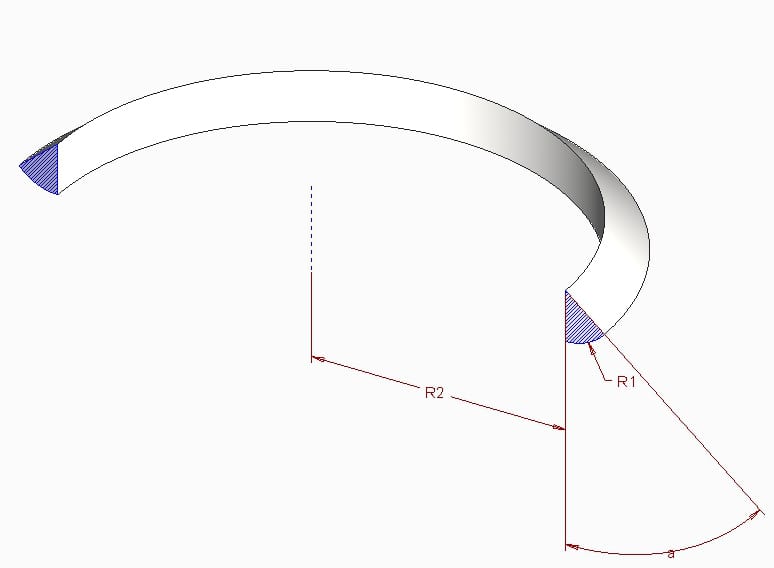
Comment calculer le volume d'un quartier de tore (au lieu que la section du tore soit un cercle, la section est un quartier d'angle α)
Publié le 13/05/2015 à 14:14:33 - Auteur : Bastien L.
REPONSES :
Le volume d'un tore est égal à V = 2π²r²R en posant r le rayon de disque du tore et R le rayon du centre "pneu" formé par le tore au centre du disque de rayon r.
on a V = πr² × 2πR où 2πR la longueur du tore
en fait on intègre πr² sur 0 à 2πR, V = ∫02πR πr²dR
pour votre section d'angle α et de surface π × α × r² ÷ 360, la formule devient :
V = απr² ÷ 360 × 2πR = 2απ²r²R ÷ 360
Réponse publiée le 14/05/2015 à 12:32:04 - Auteur : Le webmaster
C'est tout à fait faux! Le problème est plus complexe car dans votre formule R est en réalité pris au barycentre de la section de disque. Il dépend donc de alpha et de l'angle initial qui définirait l'orientation de la portion de disque dans le repère cylindrique du tore (http://villemin.gerard.free.fr/GeomLAV/Cercle/aaaAIRE/Secteur_fichiers/image017.jpg sur cette image l'angle beta)
Dans le cas particulier de beta=0 on aurait R_cdg = R + 2r/(3alpha)sin(alpha) (avec R le rayon du centre "pneu" formé par le tore au centre du disque de rayon r)
Donc dans vos notation :
V = 2alpha pi² r² (R+2r/(3alpha) sin(alpha))
Réponse publiée le 22/03/2021 à 12:13:17 - Auteur : C. robitaille

