Rechercher un outil (en entrant un mot clé):
Calculer l'aire d'un anneau (couronne)
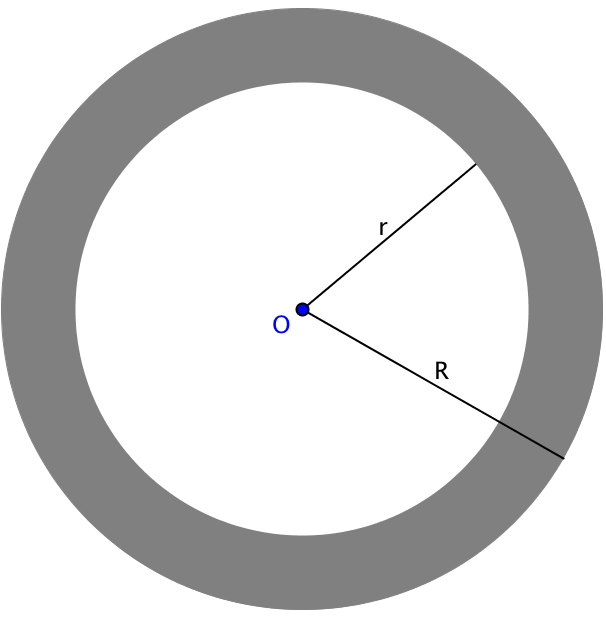
Une couronne est la surface délimitée par deux cercles de même centre mais de rayons différents. Ces cercles sont appelés cercles concentriques.
Formule de l’aire :
L’aire de la surface définie par une couronne est donnée par la formule :
Aire = π (R² - r²)
Explications des termes :
- R : Rayon du cercle extérieur (le plus grand).
- r : Rayon du cercle intérieur (le plus petit).
- π : Constante mathématique (≈ 3,14159).
Interprétation :
La formule soustrait l’aire du cercle intérieur (π r²) de l’aire du cercle extérieur
(π R²) pour obtenir l’aire de la couronne.
Exemple :
Pour une couronne avec :
- R = 10 cm
- r = 6 cm
L’aire est :
Aire = π (10² - 6²)
= π (100 - 36)
= π × 64
= 201,06 cm² (en arrondissant).
Applications :
Le calcul de l’aire d’une couronne est utile dans de nombreux contextes, notamment en géométrie, en architecture, et dans la conception de pièces mécaniques.
Calculer l'aire d'un anneau :
L'aire d'une couronne est toujours exprimée dans l’unité au carré des rayons. Par exemple :
- Si les rayons sont donnés en centimètres (cm), l’aire sera en cm2.
- Si les rayons sont donnés en mètres (m), l’aire sera en m2.
Une curieuse formule pour calculer l'aire d'une couronne
Une autre manière de calculer l’aire d’une couronne consiste à utiliser :
h = R - r (largeur de la couronne) et rm = (R + r) / 2 (rayon moyen).
La formule devient alors :
Aire = 2π × h × rm
Démonstration :
Partons de la formule classique :
π (R² - r²)
En développant, nous avons :
π ((R - r) × (R + r))
Factorisons avec la largeur h et le rayon moyen rm :
π × h × 2rm
Finalement :
Aire = 2π × h × rm
Illustration :
Voici une représentation visuelle de la couronne :
Applications :
Cette approche alternative est particulièrement utile pour visualiser la couronne comme une bande rectangulaire de largeur h et de longueur 2πrm déroulée en ligne droite.

