Rechercher un outil (en entrant un mot clé):
La Valeur Actuelle Nette (VAN), ou Net Present Value (NPV) en anglais, est l'indicateur clé pour mesurer la rentabilité d'un projet d'investissement en tenant compte de la valeur temporelle de l'argent.
Pourquoi calculer la VAN ?
- ✅ Déterminer si un investissement crée de la valeur
- ✅ Comparer différents projets d'investissement
- ✅ Prendre en compte le facteur temps et le risque
- ✅ Optimiser vos décisions financières
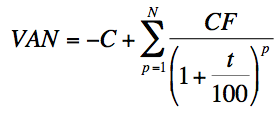
Composantes de la formule :
- C : Capital initial investi (sortie de trésorerie)
- CFt : Flux de trésorerie net à la période t
- i : Taux d'actualisation (reflétant le coût du capital et le risque)
- N : Nombre total de périodes
Calculateur de VAN avec taux croissant
Interprétation des résultats
| VAN | Interprétation | Décision |
|---|---|---|
| > 0 | L'investissement génère plus que le rendement exigé | Projet à accepter |
| = 0 | L'investissement génère exactement le rendement exigé | Projet acceptable |
| < 0 | L'investissement ne couvre pas le rendement exigé | Projet à rejeter |
Applications concrètes
🚀 Lancement de produit
Évaluer la rentabilité d'un nouveau produit en actualisant les flux futurs
🏗️ Projet immobilier
Calculer la rentabilité d'un investissement locatif
💻 Projet informatique
Estimer le ROI d'un nouveau système informatique
💡 Bon à savoir : La VAN est particulièrement utile pour les investissements à long terme où les flux de trésorerie sont étalés sur plusieurs années. Plus le taux d'actualisation est élevé, plus la VAN diminue, reflétant un risque perçu plus important.
Exemple concret de calcul de Valeur Actuelle Nette
Cas n°1 : Investissement avec retour progressif
Prenons l'exemple d'un projet nécessitant un investissement initial de 10 000 €, avec des flux de trésorerie anticipés sur 5 ans :
- Année 1 : 2 000 €
- Année 2 : 2 500 €
- Années 3 à 5 : 3 000 € chaque année
Avec un taux d'actualisation de 10%, le calcul se décompose ainsi :
| Année | Flux brut | Flux actualisé | VAN cumulative |
|---|---|---|---|
| 0 (Investissement) | -10 000,00 € | -10 000,00 € | -10 000,00 € |
| 1 | +2 000,00 € | +1 818,18 € | -8 181,82 € |
| 2 | +2 500,00 € | +2 066,12 € | -6 115,70 € |
| 3 | +3 000,00 € | +2 253,94 € | -3 861,76 € |
| 4 | +3 000,00 € | +2 049,04 € | -1 812,72 € |
| 5 | +3 000,00 € | +1 862,76 € | +50,05 € |
Détail du calcul :
VAN = -10 000 + (2 000/1,101) + (2 500/1,102) + (3 000/1,103) + (3 000/1,104) + (3 000/1,105)
VAN = 50,05 € (valeur arrondie)
📈 Interprétation : La VAN étant légèrement positive (50,05 €), cet investissement est tout juste rentable au taux de 10%. Il crée une faible valeur supplémentaire.
Cas n°2 : L'importance cruciale de l'actualisation
Considérons maintenant un projet plus important :
- Investissement initial : 300 000 €
- Flux sur 7 ans : -50 000 €, -25 000 €, +25 000 €, +50 000 €, +75 000 €, +100 000 €, +200 000 €
À première vue, la somme simple des flux donne :
-300 000 - 50 000 - 25 000 + 25 000 + 50 000 + 75 000 + 100 000 + 200 000 = +75 000 €
Ce qui semblerait attractif.
Mais en calculant la VAN avec un taux d'actualisation modeste de 3,5% (taux proche de l'inflation) :
VAN = -3 830,02 €
📉 Réalité : Une fois les flux actualisés, le projet détruit de la valeur. Cela s'explique par :
- Les sorties de trésorerie interviennent tôt (elles sont moins actualisées)
- Les entrées importantes arrivent trop tard (leur valeur actuelle est fortement réduite)
Ce que nous apprend cet exemple :
- La VAN donne une vision plus précise que la simple somme des flux
- La temporalité des flux est cruciale - un euro aujourd'hui vaut plus qu'un euro demain
- Même un projet avec flux totaux positifs peut être non rentable après actualisation
- Le choix du taux d'actualisation influence fortement le résultat

