Rechercher un outil (en entrant un mot clé):
Diviser deux entiers "à la main"
Voici un outil particulièrement utile pour plusieurs raisons. Tout d'abord, il vous permet de diviser deux grands entiers — pouvant contenir plusieurs dizaines de chiffres — avec une précision fixée, une fonctionnalité que les calculatrices classiques ne permettent généralement pas.
Ensuite, cet outil vous permet d'effectuer des divisions posées comme si vous les faisiez "à la main". Il peut ainsi être très utile pour aider vos enfants, en primaire ou en sixième, à comprendre le processus et à corriger leurs éventuelles erreurs.
* Nombre de chiffres après la virgule
Exemple : Division de 22 par 7 pour approximer le nombre π (pi)
La division de 22 par 7 donne une approximation du nombre π avec un résultat de 3,14 en gardant 2 décimales correctes.
Étapes de la division :
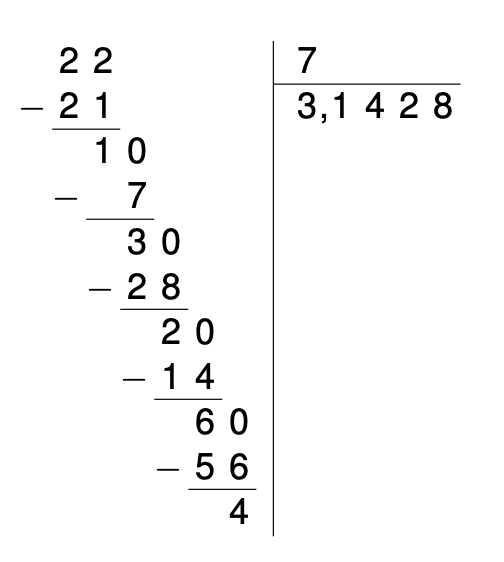
Explication détaillée :
- On commence par diviser 22 par 7 pour obtenir 3 avec un reste de 1.
- On ajoute un 0 après le reste (1) pour continuer la division avec 10.
- 10 divisé par 7 donne 1, avec un reste de 3. On continue de cette manière en ajoutant un 0 au reste à chaque étape.
- On obtient ainsi les décimales suivantes en poursuivant la division.
Note : Effectuer des divisions à la main est un bon exercice pour visualiser les décimales et comprendre la répétition des chiffres dans les divisions inexactes.
Exemple : Division de 56 par 9
La division de 56 par 9 donne un résultat périodique avec un quotient de 6.222....
Étapes de la division :

Explication détaillée :
- On commence par diviser 56 par 9, ce qui donne 6 avec un reste de 2.
- On ajoute un 0 au reste (2), obtenant ainsi 20.
- Ensuite, on divise 20 par 9, ce qui donne 2 avec un reste de 2 encore.
- Ce processus continue avec le reste de 2, ajoutant un 0 chaque fois pour obtenir 20 et diviser encore par 9.
- On obtient ainsi un résultat périodique de 6.222... car la séquence 2 se répète indéfiniment.
Note : Ce type de division, où le reste se répète de manière cyclique, crée un nombre décimal périodique. Cela signifie que le nombre a une séquence répétitive infinie dans sa partie décimale.

