Rechercher un outil (en entrant un mot clé):
Tracer la courbe représentative d'une fonction
Cet outil permet d'obtenir la courbe représentative d'une fonction de variable x. L'expression de la fonction doit être de variable x et de la forme, par exemple, ƒ(x) = 3x + 2 , avec x pour variable. Les termes et les fonctions acceptés sont :
- les opérateurs simples et parenthèses + – * / ( )
- la fonction puissance xn s'écrit pow(x,n). Exemple x5 s'écrit pow(x,5) etc;
- seulement les puissances deux et trois de x peuvent d'écrire x^2 et x^3
- la fonction racine carrée √x s'écrit pow(x,0.5) ou pow(x,1/2);
- la fonction exponentielle ex s'écrit exp(x);
- la fonction logarithme népérien : log(x);
- les fonctions sinus, cosinus et tangente s'écrivent respectivement : sin(x), cos(x) et tan(x).
Voir plus bas sur cette page pour :
- les conseils de rédaction des fonctions;
- le choix du repère;
- les limites de l'outil.
* En sélectionnant cette option, lesles maximums et minimums n'apparaitront plus nécessairement sur le graphique.
Exemples de courbes obtenues grâce à l'outil
Vous pouvez copier/coller ces exemples dans l'outil.
Courbe de la fonction ƒ(x) = x+2 sur [–4 ; 4].
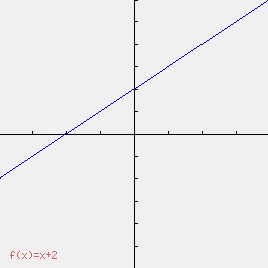
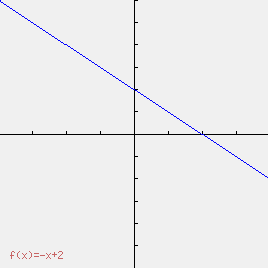
Courbe de la fonction ƒ(x) = –x+2 sur [–4;4].
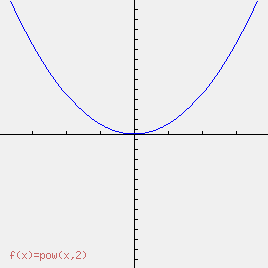
Courbe de la fonction carrée ƒ(x) = pow(x,2) sur [–4 ; 4].
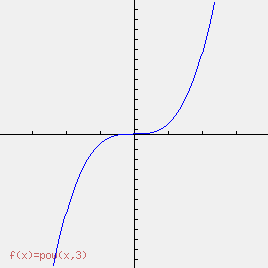
Courbe de la fonction cube ƒ(x) = pow(x,3) sur [–4;4].
Courbe de la fonction racine carrée ƒ(x) = √x = x^(1/2) = pow(x,0.5) sur [0 ; 4,5].
.png)
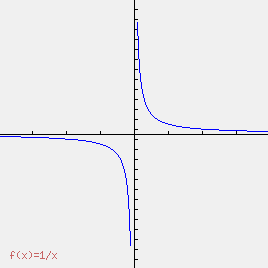
Courbe de la fonction inverse ƒ(x) = 1/x sur [–4;4].
Courbe de la fonction de homographique ƒ(x) = (x+1)/(x+2) sur le repère [–4 ; 4].
÷(x+2).png)
La fonction est définie sur ]−∞ ; −2[ ∪ ]−2 ; +∞[, la courbe admet une asymptote verticale d'équation x = −2.
Courbe de la fonction logarithme népérien ƒ(x) = ln(x) sur le repère [–0.5;10];
.png)
La fonction est définie sur ]0 ; +∞[ la courbe admet une asymptote verticale d'équation x = 0 et limx→0ln(x)=−∞.
Courbe de la fonction de ƒ(x)=(x-2)(x-1)(x+1)(x+2) sur le repère [–2.5;2.5];
(x-1)(x+1)(x+2).png)
Courbe de la fonction de ƒ(x)=(6x-2)(x-1)(x+1)(x+2) sur le repère [–3;3];
(x-1)(x+1)(x+2).png)
Choisir son repère
Vous pouvez choisir l'intervalle de définition sur l'axe des abscisses (les valeurs entre lesquelles varie x) sur lequel tracer la courbe de votre fonction. Cet intervalle est généralement donné dans l'énoncé de l'exercice. Si ce n'est pas le cas, choisissez un intervalle assez large. L'outil déterminera en fonction de votre intervalle le meilleur rapport pour l'axe des ordonnées, afin que les maximums ou les minimums (les plus grandes ou plus petites valeurs de ƒ(x)) de la fonction apparaissent.
Conseil de rédaction des fonctions
Comme pour tous les outils, vous pouvez toujours le mettre en défaut. L'outil interprète les fonctions à une variable et l'inconnue doit être la lettre x.
Voici quelques exemples de rédaction de fonctions :
|
|
