Rechercher un sujet parmi les questions (en entrant un mot clé):
Surface de l'intersection de disques
Considérons deux cercles de rayons R et R' (avec R > R') qui soient sécants en deux points. L'intersections des deux cercles délimitent une surface (en forme de lentille), comment calculer l'aire de cette surface ?
Publié le 28/02/2013 à 11:18:43 - Auteur : Webmaster
REPONSES :
Soient deux cercles C et C', de rayons R et R' (avec R > R), de centres respectifs O et O' (O' à l'extérieur du cercle C).
Nommons D la distance des deux centres, on a D = OO'. Fixons D < R + R' alors les deux cercles sont sécantes en 2 points (P et Q) et l'intersection de leur disque respectif est une surface (lentille) dont l'aire S est strictement positive.
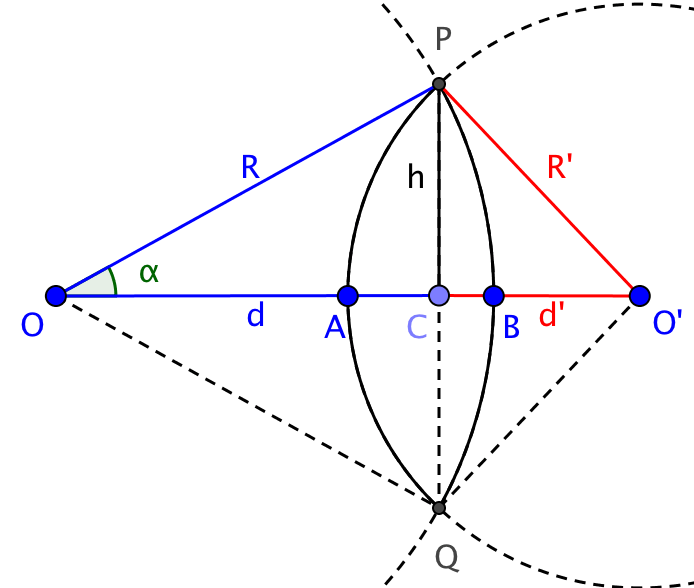
Comment calculer S l'aire de la surface de l'intersection en fonction de R, R' et D ?
Réponse publiée le 28/02/2013 à 15:55:05 - Auteur : Webmaster
Les valeurs connues sont la distance D des 2 centres et les 2 rayons des deux cercles R et R'.
On a : D = OO' , d = OC , d' = CO' et h = CP.
On a : D = d + d'
Calcul de d et d'
Dans le triangle OCP rectangle en C on a : cos (α) = d/R et α = arccos(d/R).
En utilisant les formules de trigonométrie dans le triangle quelconque OO'P on obtient :
R'² = R² + D² − 2RD.cos (α)
R'² = R² + D² − 2RD.d/R
R'² = R² + D² − 2Dd
d'où d = ( R² + D² − R'² ) / 2D
et d' = D − d
Nous pouvons calculer l'aire du segment de disque issu du cercle C.
aire du secteur angulaire d'angle 2α − l'aire du triangle OPQ
R².2.α/2 − (d.2h)/2
R².α − d.h (dans le triangle OCP rectangle en C on a : h = √(R² − d²) )
d'où on obtient R².arccos(d/R) − d.√(R² − d²)
On obtient de même pour le second segment de disque : R'².arccos(d'/R') − d'.√(R'² − d'²)
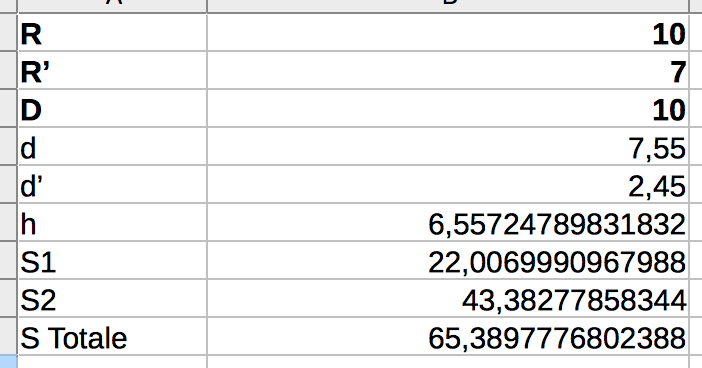
Application : Calculer l'aire d'une lentille avec D = 10 , R = 10 et R' = 7.
d = (10² + 10² − 7²) / 20 = 7,55
d' = 10 − 7,55 = 2,45
h = √(10² − 7,55²) = 6,55
R².arccos(d/R) − d.h = 22
R'².arccos(d'/R') − d'.h = 43,38
Réponse publiée le 17/07/2017 à 10:58:32 - Auteur : Webmaster
On peut facilement vérifier tout ça en utilisant un tableur et profiter pour faire quelques essais.
Réponse publiée le 17/07/2017 à 10:59:43 - Auteur : webmaster
Bonjour, j'essaie de vérifier le calcul sur un cas particulier. Deux cercles identiques, la circonférence de l'un passant au centre de l'autre et vice versa.
Donc R=R'=d=d'=D/2.
L'arccos de 1 me donne zéro... et la racine idem... donc je suppose qu'il y a quelque chose qui m'échappe.
Réponse publiée le 10/09/2017 à 19:31:20 - Auteur : Adrien
Bonjour, oui les distances d et d' ne sont pas égales à R et R' !
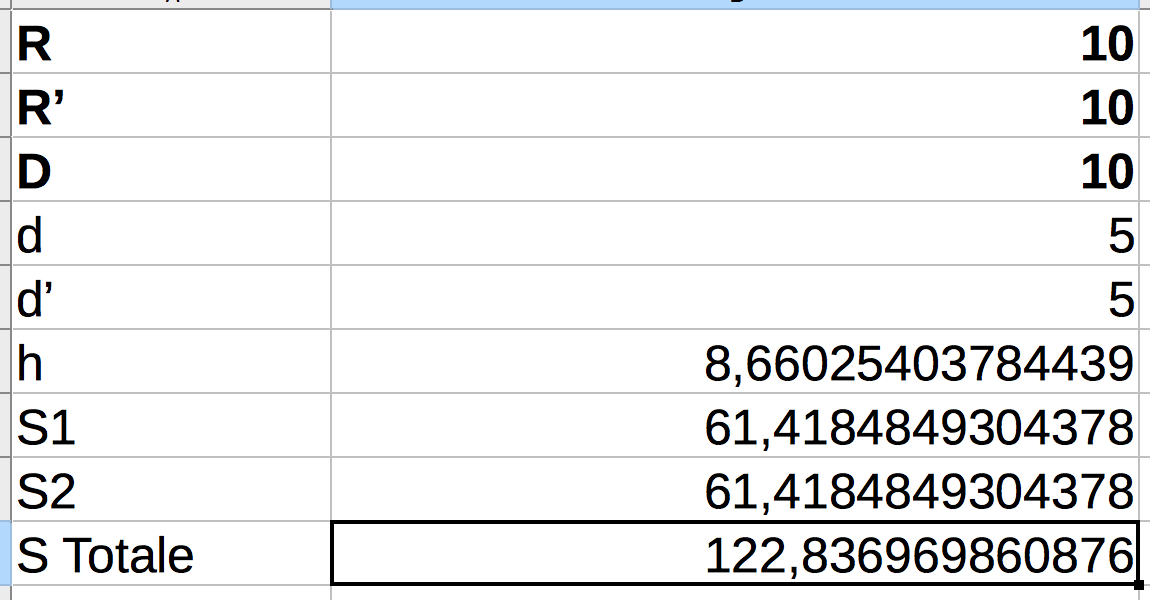
On a D = R = R' et d = d' = D/2
Par exemple avec R = R' = D = 10 on a :
Réponse publiée le 11/09/2017 à 07:39:06 - Auteur : Le webmaster
en effet, j'ai été trop vite. Merci beaucoup.
Réponse publiée le 11/09/2017 à 22:00:13 - Auteur :
Est il possible de résoudre ce problème (semblable à celui de la chèvre qui ne doit brouter que la moitié d'un pré rond) en passant par des intégrales déterminant des surfaces de cercles s'interceptant.
Merci.
Réponse publiée le 11/05/2020 à 00:25:26 - Auteur : Didier D.
oui comme à cette page : https://calculis.net/q/intersection-de-2-disques-334
Réponse publiée le 14/05/2020 à 13:47:03 - Auteur : Le webmaster
Bonjour,
Je cherche à visualiser des pourcentages sous forme de cercles entrecoupés au lieu de camanberts pour un projet artistique en céramique.
Je dispose d'un cercle emporte pièces de 10cm de diamètre (5 de rayon)
Je veux representer des données environnementales en pourcents.
Par exemple, 60%.quelle distance en cm entre les deux centres de cercles oo' dois t il y avoir pour couper le premier cercle 60% de sa surface...
Les deux cercles ont le même diamètre
Réponse publiée le 02/04/2021 à 23:40:31 - Auteur : Adrián

