Rechercher un sujet parmi les questions (en entrant un mot clé):
Egalité d'aires
Soit un carré ABCD et E un point appartenant au segment [AB].
On construit le carré AEFG et le triangle FBC. Comment positionner le point E afin que les aires du carré AEFG et du triangle FBC soient égales ?
Publié le 26/03/2013 à 14:04:26 - Auteur : Webmaster
REPONSES :
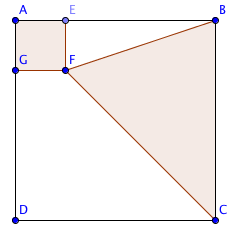
Ce genre de problème est utilisé en TICE. Si on étudie la figure avec géogébras, il en fait assez évidement que les aires deviennent égales lorsque E est au milieu du segment [AB].
Démonstration :
Nommons x la mesure du segment [AE]. x peut varier de 0 à AB = 10.
L'aire du carré AEFG est égale à : x² et l'aire du triangle est égale à 10 × (10 − x ) ÷ 2 = 5(10 − x )
il suffit de résoudre l'équation suivante :
Nous pouvons utiliser l'outil de la page suivante : http://calculis.net/resoudre-equation-second-degre afin de résoudre l'équation du second degré et nous obtenons :
Le discriminant est égal à (-5)² − 4(−1 × 50) = 25 + 200 = 225 > 0 et √225 = 15 donc l'équation :
−x² −5x + 50 = 0 admet 2 solutions réélles (5 + 15) / −2 = −10 et (5 − 15) / −2 = 5.
x ne peut varier de 0 à 10 alors la seule solution possible est x = 5.
Donc pour que les aires soient égales, il suffit bien que E soit le milieu de [AB].
Réponse publiée le 26/03/2013 à 14:59:23 - Auteur : Webmaster

