Rechercher un sujet parmi les questions (en entrant un mot clé):
Surface d'un cône
Comment calculer la surface latérale d'un cône ? Un cône de révolution est un solide engendré par la révolution d'un triangle rectangle autour de l'un des côtés de l'angle droit.
Publié le 18/02/2013 à 00:14:11 - Auteur : Webmaster
REPONSES :
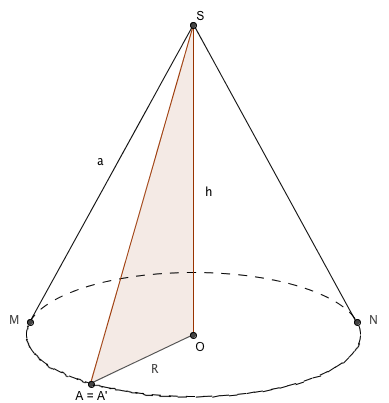
Nommons les valeurs importantes du cône, soit a l'apothème, h la hauteur et R le rayon de sa base.
Fendons le cône selon l'apothème SA par exemple et déroulons cette sur face sur un plan, nous obtenons la figure suivante :
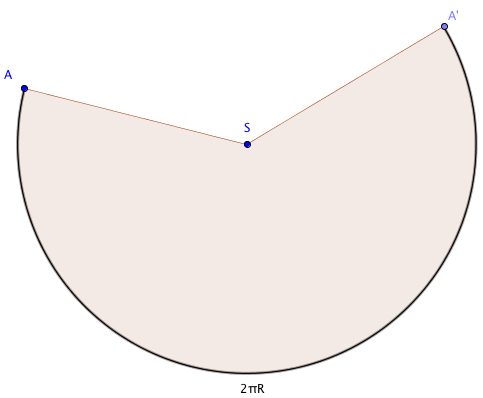
Nous allons exprimer la longueur L de la base.
L = 2πR le circonférence de la base du cône de rayon R
et
L = (2πa × α)÷360 la longueur d'un arc de cercle de rayon a et d'angle α l'angle ASA'.
Nous pouvons donc déterminer l'angle α selon R et a comme suit :
(2πa × α)÷360 = 2?R
(a × α)÷360 = R
d'où
Nous pouvons donc calculer l'aire de la surface latérale S du cône celle-ci est égale à l'aire du secteur circulaire d'angle ? et de rayon a :
S = π × a² × α ÷ 360, on applique la formule d'un secteur circulaire
S = π × a² × R × 360 ÷ a ÷360, on remplace ? par R × 360 ÷ a
En simplifiant on obtient :
Réponse publiée le 18/02/2013 à 15:26:58 - Auteur : Webmaster

