Rechercher un sujet parmi les questions (en entrant un mot clé):
Calculer l'aire d'un croissant
Comment calculer l'aire de la surface d'un croissant ?
Publié le 24/02/2013 à 13:03:30 - Auteur : Webmaster
REPONSES :
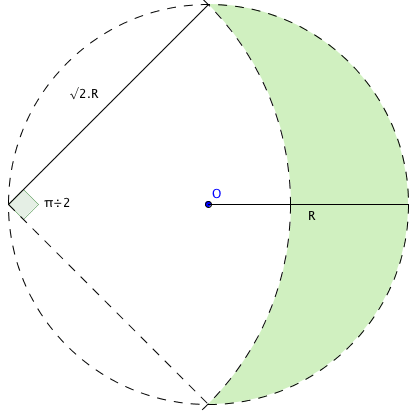
Pour calculer l'aire de la surface du croissant il faut au demi-disque de rayon R et de surface ½πR², lui soustraire le segment de disque issue de l'angle π/2 et de corde 2R.
Le rayon du segment est égal à : √(R² + R²) = √2.R et l'aire de sa surface est égale à : ½(√2.R)²(α - sinα) voir cette page http://calculis.net/aire/segment-disque pour la démonstration.
De là l'aire de la surface du croissant devient :
½πR² - ½(√2.R)²(α - sinα) avec α = π/2 et sin(π/2) = 1
½πR² - ½.2.R².π/2 + ½.2.R²= ½πR² - ½πR² + R² = R²
L'aire surface de ce croissant ainsi construit est égal à R² résultat tout de même assez surprenant de simplicité !
Réponse publiée le 24/02/2013 à 14:09:23 - Auteur : Webmaster
Voir aussi cette page connexe : calculis.net/q/aire-intersection-disques-35
Réponse publiée le 31/07/2019 à 09:12:26 - Auteur : Le webmaster

