Rechercher un outil (en entrant un mot clé):
Utilisons le Théorème de Thalès
Théorème de Thalès
Dans les 3 configurations nous avons :
Les droites (BM) et (CN) sont sécantes en A.
Les droites (BC) et (MN) sont parallèles.
Alors nous pouvons écrire les égalités suivantes :
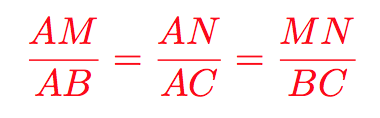
Afin de bien utiliser l'outil, il faut identifier les valeurs connues comme dans les configurations ci‑dessus. Vous pouvez par exemple renommer les points de votre exercice comme nos figures en utilisant : A, B, C, M et N.
* Il faut connaitre au moins les 2 valeurs d'un même rapport et une troisième valeur afin de pouvoir appliquer le théorème de Thalès !
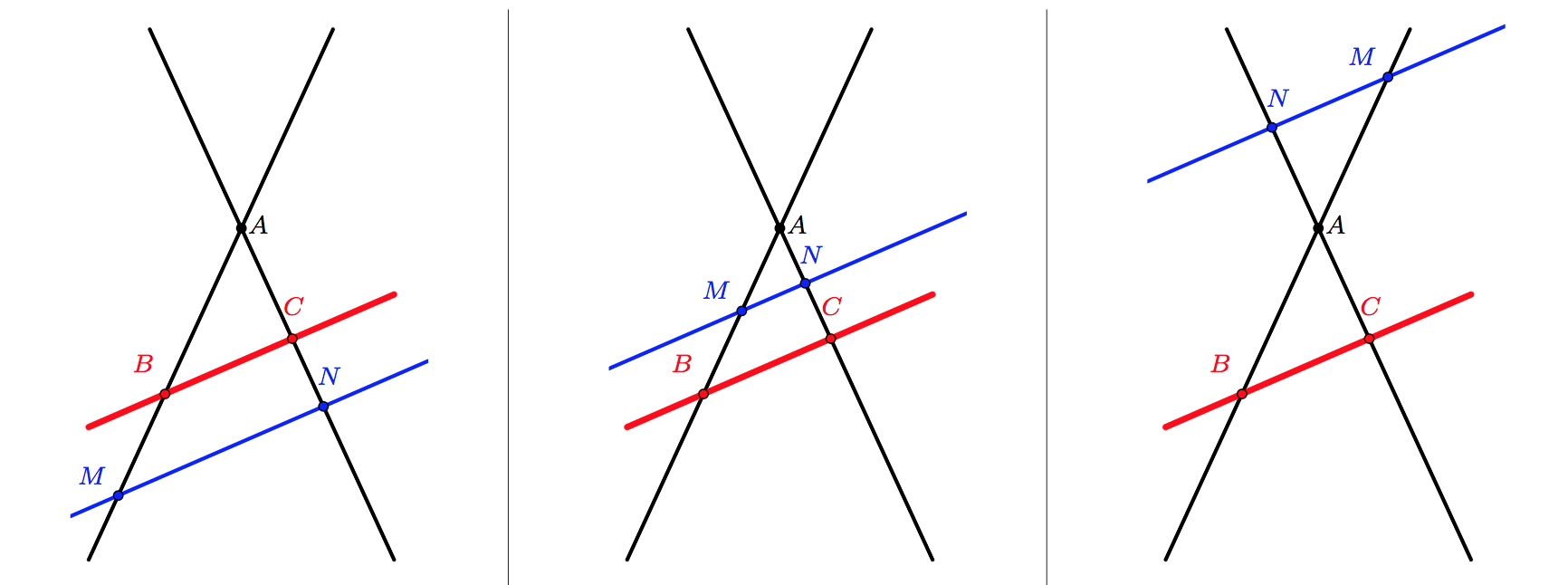
Exemple d'utilisation du théorème de Thalès :
Soit un triangle ABC. I un point du segment [AB] et J un point du segment [AC]. On a (IJ) // (BC).
Dans chacun des cas suivants :
a) AI = 4; IB = 12; AJ = 5 et BC = 14
Calculer en justifiant AB, AC et IJ.
b) AI = 4,5; AC = 8,4; IJ = 5; BC = 14
Calculer AB et AJ.
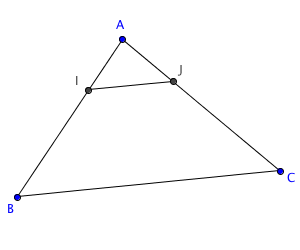
Solutions : Pour utiliser l'outil de cette page il suffit de remarquer que les points I et J dans l'énoncé jouent les rôles respectifs des points M et N de la configuration de l'outil.
a) AB = AI + IB = 4 + 12 = 16.
Vous pouvez entrer les valeurs suivantes AI = 4; AB = 16; AJ = 5 et BC = 14 en utilisant la remarque précèdente. Cela donne AI = AM = 4; AB = 16; AJ = AN = 5 et BC = 1. L'outil nous donne comme réponses :
Nous pouvons calculer la valeur de AC :
AM / AB = AN / AC
AC = AB × AN / AM
AC = 16 × 5 ÷ 4
AC = 20.
Et nous pouvons calculer la valeur de de :
AM / AB = de / BC
de = AM × BC / AB
de = 4 × 14 / 16
de = 3,5.
Donc IJ = de = 3,5.
b) Ici, toujours en identifiant I et J comme les points M et N de la configuration de l'outil, nous pouvons entrer les valeurs suivantes : AI = AM = 4.5; AC = 8.4; IJ = de = 5 et BC = 14. Nous obtenons les résultats suivants :
Nous pouvons calculer la valeur de AB :
AM / AB = de / BC
AB = AM × BC / de
AB = 4,5 × 14 / 5
AB = 12,6.
Et nous pouvons calculer la valeur de AN :
AN / AC = de / BC
AN = de × AC / BC
AN = 5 × 8,4 / 14
AN = 3.
Donc AJ = AN = 3.

