Calculis

Transformation triangle étoile

Le théorème de Kennelly permet de transformer un circuit de 3 résistances en triangle (ou delta Δ) en un circuit de 3 résistances en étoile (ou Y). Les formules utilisées sont les suivantes :

1) Transformation triangle → étoile ( Δ → Y )

R₄ = R₁R₂ / ( R₁ + R₂ + R₃ )

R₅ = R₂R₃ / ( R₁ + R₂ + R₃ )

R₆ = R₁R₃ / ( R₁ + R₂ + R₃ )

2) Transformation étoile → triangle ( Y → Δ )

R₁ = ( R₄R₅ + R₅R₆ + R₆R₄ ) / R₅

R₂ = ( R₄R₅ + R₅R₆ + R₆R₄ ) / R₆

R₃ = ( R₄R₅ + R₅R₆ + R₆R₄ ) / R₄

triangle Δ ↔ étoile Y

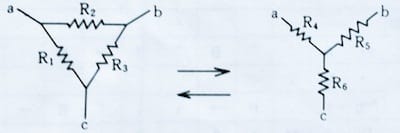
Remarque : les transformations triangles - étoiles peuvent servir à simplifier les circuits et leur études.