Rechercher un outil (en entrant un mot clé):
Développer une expression de la forme (x + y)n
Grâce à la formule du binôme de Newton, nous pouvons développer les expressions de la forme :
(x + y)n.
On obtient : (x + y)n = yn + nxyn-1 + ... +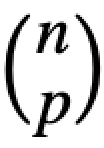 
xp yn−p + ... + nyxn-1 + xn
ou encore
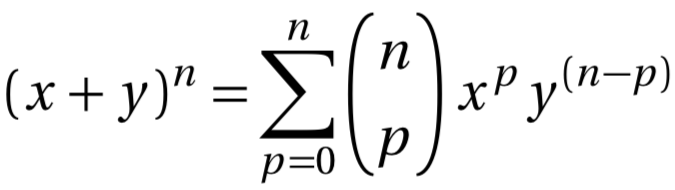
Voir la page combinaison pour la signification de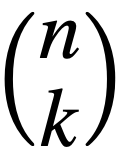 
Remarque : avec x = y = 1 on établit facilement que :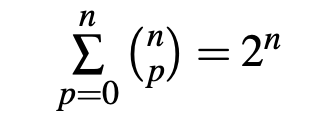 
Exemples : Identités remarquables de 3e et lycée :
(x + y)2 = x2 + 2xy + y2
(x + y)3 = x3 + 3x2y + 3xy2 + y3
(x − y)2 = x2 − 2xy + y2
(x − y)3 = x3 − 3x2y + 3xy2 − y3
Exemples : les Identités remarquables de degrès superieures de 4 à 10 :
(x + y)4 = x4 + 4x3y + 6x2y2 + 4xy3 + y4
(x + y)5 = x5 + 5x4y + 10x3y2 + 10x2y3 + 5xy4 + y5
(x + y)6 = x6 + 6x5y + 15x4y2 + 20x3y3 + 15x2y4 + 6xy5 + y6
(x + y)7 = x7 + 7x6y + 21x5y2 + 35x4y3 + 35x3y4 + 21x2y5 + 7xy6 + y7
(x + y)8 = x8 + 8x7y + 28x6y2 + 56x5y3 + 70x4y4 + 56x3y5 + 28x2y6 + 8xy7 + y8
(x + y)9 = x9 + 9x8y + 36x7y2 + 84x6y3 + 126x5y4 + 126x4y5 + 84x3y6 + 36x2y7 + 9xy8 + y9
(x + y)10 = x10 + 10x9y + 45x8y2 + 120x7y3 + 210x6y4 + 252x5y5 + 210x4y6 + 120x3y7 + 45x2y8 + 10xy9 + y10
