Rechercher un outil (en entrant un mot clé):
Calculer l'aire d'un triangle à l'aide de la formule de Héron
Soit p le périmètre d'un triangle dont les côtés ont pour mesures a, b et c.
On a donc :
\(p = a + b + c\).
On note s le demi-périmètre. On a :
\(s = \frac{1}{2} p = \frac{1}{2} (a + b + c)\).
Alors A l'aire du triangle est telle que :
\(A^2 = s (s – a)(s – b)(s – c)\)
et de là :
\(A = \sqrt {s (s – a)(s – b)(s – c)}\)
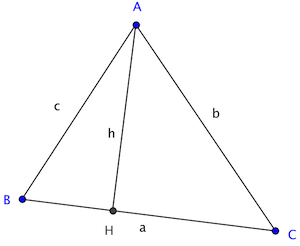
Calculer l'aire d'un triangle quelconque
L'outil calcule l'aire d'un triangle à partir des mesures de ses côtés.
Et ainsi les mesures de chaque hauteur du triangle bien qu'il soit quelconque. Il suffit de diviser par la base de chaque hauteur respective.
Dans notre exemple, la mesure de la hauteur h, issue du sommet A, est égale à :
\(h = \dfrac{2 \times Aire}{a}\)
Les commentaires :
Bonjour, excellent site. Juste une petite remarque concernant la formule de héron pour le calcul de la hauteur d'un triangle. Vous avez mis comme titre formule du héron. Ce serait plus juste de mettre formule de Héron car il s'agit de Héron d'Alexandrie. Cordialement lpino.fr
réponse : Très juste ! Merci pour cette contribution, je corrige.

