Rechercher un outil (en entrant un mot clé):
Utilisons la propriété de Pythagore dans un triangle rectangle
Grâce à cet outil, vous avez la possibilité de calculer la longueur de l'un des côtés d'un triangle rectangle.
Un triangle rectangle est un type particulier de triangle qui comprend un angle droit. Pour déterminer la longueur d'un côté, vous devrez connaître les longueurs des deux autres côtés. Cet outil vous permet de résoudre rapidement et facilement ce problème en utilisant le théorème de Pythagore. Il vous suffit d'entrer les valeurs connues, et l'outil vous donnera la longueur du côté recherché.
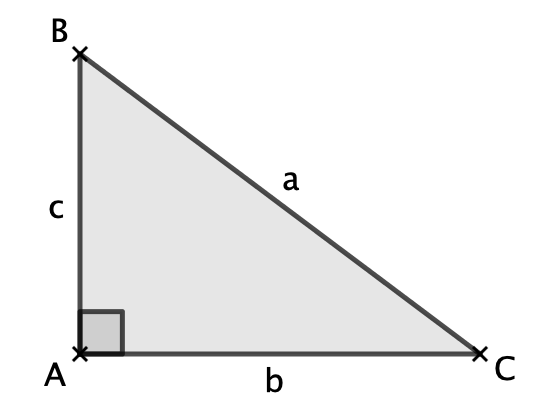
b2 + c2 = a2
avec a la mesure de l'hypoténuse, b et c les mesures des côtés de l'angle droit.
L'outil peut vérifier aussi si un triangle est rectangle en fonction de la mesure des ses 3 côtés, en appliquant la réciproque du théorème de Pythagore ou sa contraposée.
* si le triangle est rectangle
** Si vous entrez 3 valeurs, l'outil vérifie si la réciproque de la propriété de Pythagore s'applique ou non.
** Si vous entrez 2 valeurs, l'outil considère que le triangle est rectangle et calcule la troisième valeur grâce à la propriété de Pythagore.
Théorème de Pythagore
La somme des carrés des mesures des côtés de l'angle droit est égale au carré de la mesure de l'hypoténuse.
Exemple d'utilisation de la propriété de Pythagore :
Votre professeur de Mathématiques vous donne un triangle dont les mesures des côtés sont les suivantes : 10.5 cm , 8.4 cm et 6.2 cm. Il demande de vérifier si ce triangle est rectangle.
Il suffit de rentrer les 3 valeurs dans l'outil pour qu'il donne la réponse.
Réponse :
10.52 = 110.25
8.42 + 6.22 = 70.56 + 38.44 = 109
La propriété de Pythagore n'est pas vérifiée. D'après la contraposée du théorème de Pythagore, le triangle n'est pas rectangle.
Autre exemple :
On donne les mesures de deux des côtés d'un triangle rectangle. La mesure de son hypoténuse est égale à 22.1 cm et la mesure d'un des côtés de l'angle droit est égale à 8.5 cm. Quelle est la mesure du troisième côté ?
Comme le triangle est rectangle, nous pouvons appliquer la propriété de Pythagore et nous servir de l'outil en renseignant la valeur de l'hypoténuse et celle d'un côté de l'angle droit. Nous obtenons comme résultat :
- la valeur de la mesure du côté manquant est égale à : √(416.16) = 20.4 cm.

