Rechercher un outil (en entrant un mot clé):
Les relations trigonométriques dans un triangle rectangle
Ce calculateur de trigonométrie vous permet de calculer un angle ou de calculer une longueur dans un triangle rectangle, en utilisant les relations fondamentales de la trigonométrie.
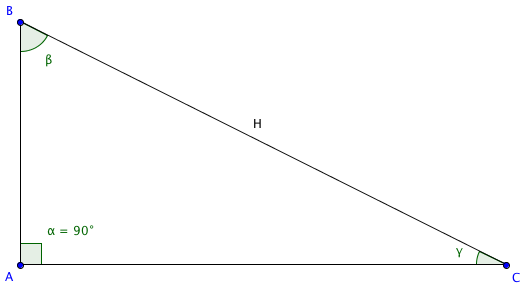
Considérons un triangle rectangle ABC, où l'angle en A est égal à α = 90°. Les angles en B et C sont respectivement notés β et γ. Grâce à ces notations, nous pouvons établir les relations trigonométriques suivantes :
- Cosinus de l'angle β :
cos(β) = adjacent / hypothénuse - Sinus de l'angle β :
sin(β) = opposé / hypothénuse - Tangente de l'angle β :
tan(β) = opposé / adjacent
Ces relations s'appliquent également pour l'angle γ en adaptant les côtés respectifs. En connaissant deux valeurs dans ces relations, que ce soient deux longueurs de côtés ou la valeur d'un angle et une longueur, nous pouvons déterminer les valeurs manquantes du triangle.
Pourquoi utiliser ces relations ? La trigonométrie dans un triangle rectangle est une méthode essentielle pour résoudre des problèmes de géométrie et de physique. Cet outil vous aide à obtenir facilement les mesures des angles et des côtés inconnus, simplifiant ainsi vos calculs et vérifications.
`cos β = {\text{côté adjacent de β}} / {\text{hypoténuse}} = {AB} / {BC}`
`sin β = {\text{côté opposé de β}} / {\text{hypoténuse}} = {AC} / {BC}`
`tan β = {\text{côté opposé de β}} / {\text{côté adjacent de β}} = {AC} / {AB}`
Nous avons les relations équivalentes pour l'angle γ :
`cos γ = {\text{côté adjacent de γ}} / {\text{hypoténuse}} = {AC} / {BC}`
`sin γ = {\text{côté opposé de γ}} / {\text{hypoténuse}} = {AB} / {BC}`
`tan γ = {\text{côté opposé de γ}} / {\text{côté adjacent de γ}} = {AB} / {AC}`
L'outil ci-dessus détermine, à partir de deux valeurs connues, quelles sont les relations trigonométriques dans le triangle rectangle à utiliser et calcule ensuite les valeurs inconnues.
Que signifie SOHCAHTOA ?
Pourquoi cette page s'appelle SOHCAHTOA ? C'est un procédé mnémotechnique qui permet de retenir facilement les relations trigonométriques dans le triangle rectangle :
SOH correspond à : Sin (angle) = `{\text{Opposé}} / {\text{Hypoténuse}}` ;
CAH correspond à : Cos (angle) = `{\text{Adjacent}} / {\text{Hypoténuse}}` ;
TOA correspond à : Tan (angle) = `{\text{Opposé}} / {\text{Adjacent}}`.
Valeurs remarquables des cos, sin et tan :
Angle nul :
cos 0 = 1 ; sin 0 = 0 ; tan 0 = 0
Angle de 45° :
cos 45° = sin 45° = √2 / 2 ≈ 0.707
tan 45° = 1
Angles de 60° et de 30° :
sin 30° = cos 60° = 1/2
cos 30° = sin 60° = √3 / 2 ≈ 0.866
tan 60° = √3 ≈1.732
tan 30° =√3 / 3 ≈ 0.577
Correpondance entre degrés et radians :
| degrés | 0 | 30 | 45 | 60 | 90 |
| radian | 0 | π/6 | π/4 | π/3 | π/2 |
Exemple de résolution d'un exercice de trigonométrie dans un triangle rectangle à l'aide de l'outil de cette page.
Soit DEF un triangle tel que : EF = 6 cm, l'angle en E est égal à 37° et l'angle en D est égal à 53°.
1) Montrer que le triangle DEF est rectangle en F.
2) Calculer DE et DF (donner les résultats à 0,1 cm près).
1) L'angle en F est égal à 180°− 37° − 53° = 90°. Le triangle est bien rectangle en F, nous pouvons donc utiliser les relations trigonométriques dans le triangle réctangle DEF et l'outil de cette page.
Remarques :
[EF] est le côté adjacent de l'angle en E et le côté opposé à l'angle en D. [ED] est l'hypoténuse du triangle.
2) Renseignons les valeurs suivantes dans l'outil : angle 37° et côté adjacent = 6 ; Nous obtenons comme réponse :
Nous connaissons la valeur de l'angle et la valeur de son côté adjacent, nous pouvons utiliser les relations suivantes : cos (angle) = côté adjacent / hypoténuse , afin de déterminer la valeur de l'hypoténuse.
hypoténuse = côté adjacent / cos (angle)
hypoténuse = 6 / cos (37°)
hypoténuse = 6 / 0.79863551004729
hypoténuse = 7.5128139489374
tan (angle) = côté opposé / côté adjacent , afin de déterminer la valeur du côté opposé
côté opposé = tan angle) × côté adjacent
côté opposé = tan (37°) × 6
côté opposé = 0.75355405010279 × 6
côté opposé = 4.5213243006168
Donc la mesure de l'hypoténuse [ED] est égale à 7.5 cm (à 0,1 cm près) et la mesure de [DF] est égale à 4.5 cm (à 0,1 cm près).
On peut vérifier que 4.52 + 62 est bien égal à 7.52 . Les mesures trouvées vérifient la propriété de Pythagore.

