Rechercher un outil (en entrant un mot clé):
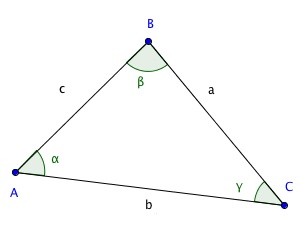
Utilisons les relations trigonométriques d'un triangle quelconque
Grâce à cet outil, nous pouvons calculer à peu près tout dans un triangle quelconque : la mesure des longueurs des différents côtés, la mesure de ses angles, son aire, son périmètre et même la valeur des longueurs de ses hauteurs. C'est vraiment le calculateur du triangle !
Théorème d'Al-Kashi
Soit un triangle quelconque ABC. On note a,b et c les mesures respectives des longueurs des segments [BC], [AC] et [AB] et α, β et γ les mesures des angles respectifs en A, en B et en C.
D'après le théorème d'Al-Kashi (ou loi des cosinus), nous avons les relations suivantes :
a² = b² + c² − 2bc.cos(α)
b² = a² + c² − 2ac.cos(β)
c² = a² + b² − 2ab.cos(γ)
* Soit les mesures des 3 côtés ou 1 angle et les 2 côtés adjacents ou 1 angle, le côté opposé et 1 côté adjacent ou 2 angles et le côté commun ou encore 2 angles et un côté non commun.
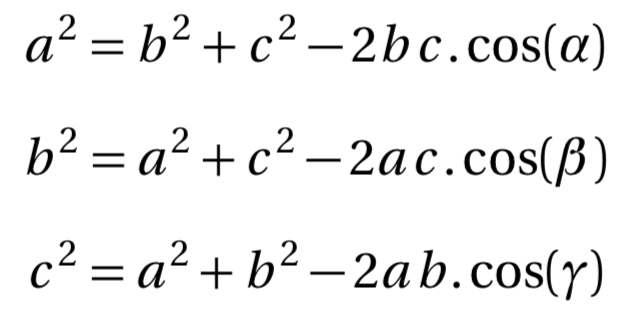
Autres formules : Lois des sinus
Le calculateur utilise aussi les formules, appelées "loi des sinus", valables dans un triangle quelconque :
a / sin(α) = b / sin(β) = c / sin(γ)
Exemple d'utilisation des relations trigonométriques dans le triangle quelconque :
DEF est un triangle tel que DE = 4cm ; EF = 6 cm et l'angle en E est égale à 70°.
1) Calculer l'aire de DEF
2) Calculer la mesure de la hauteur issue de E.
3) Calculer les mesures des angles en D et en F à 10−1 près.
En connaissant 1 angle et les 2 côtés adjaçents, nous pouvons calculer :
1)
l'aire du triangle = 4 × 6 × sin(70) ÷ 2
l'aire du triangle = 11.28
2)
DF = √(DE² + EF² − 2×DE×EF×cos(70))
DF = √(4² + 6² − 2×4×6×cos(70))
DF = √(16 + 36 − 16.416966879632)
DF = 5.97 cm
d'où la hauteur issue de E = 11.28 × 2 ÷ 5.97 = 3.78
3) et les angles : β = 39° γ = 71°
Autre exemple : Soit un triangle ABC quelconque dont les mesures des cotés a,b et c sont égales à :
a = 6 cm, b = 4 cm et c = 5 cm. Calculer les mesures des angles en A, B et C.
Le calculateur nous donne :
α = arccos[(b² + c² − a²) ÷ 2bc]
α = arccos[(4² + 5² − 6²) ÷ (2 × 4 × 5)]
α = arccos[0.125]
α = 82.82°
β = arccos[(a² + c² − b²) ÷ 2ac]
β = arccos[(6² + 5² − 4²) ÷ (2 × 6 × 5)]
β = arccos[0.75]
β = 41.41°
γ = arccos[(a² + b² − c²) ÷ 2ab]
γ = arccos[(6² + 4² − 5²) ÷ (2 × 6 × 4)]
γ = arccos[0.5625]
γ = 55.77° .
Nous pouvons obtenir aussi :
- le périmètre : 15 et en notant s = 7.5 le demi-périmètre
- l'aire du triangle par la formule de Héron : √[7.5 × (7.5 − 6) × (7.5 − 4) × (7.5 − 5)] = √98.4375 = 9.92 cm².

