Rechercher un outil (en entrant un mot clé):
Calculer des probabilités conditionnelles
Compléter un arbre de probabilité conditionnelle à deux épreuves et calculer l'arbre inverse correspondant.
En utilisant la formule de Bayes : \(P_A(B) = \dfrac{P(A \cap B)}{P(A)}\)
Probabilité conditionnelle
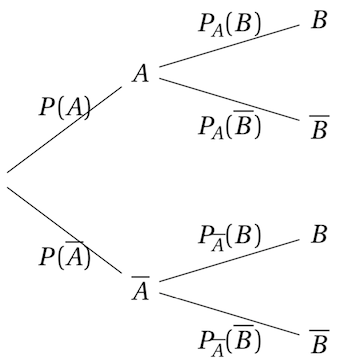
On considère un arbre pondéré à deux épreuves A et B, l'on connait les valeurs de \(P(A)\), \(P_A(B)\) et \(P_\overline{A}(B)\). Il est alors possible de compléter l'arbre et même de l'inverser.
Pour compléter l'arbre, il suffit d'utiliser :
\(P(\overline{E}) = 1 - P(E)\)
Pour inverser un arbre de probabilité, il faut calculer,en plus de P(B), \(P_B(A)\) et pour cela utiliser la relation :
\( P(A \cap B) = P_A(B) \times P(A) = P_B(A) \times P(B) \)
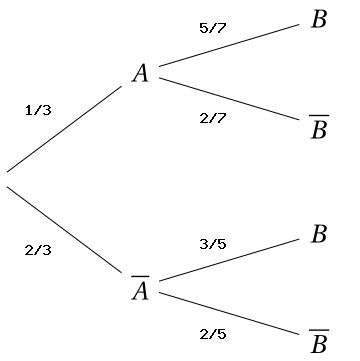
Exemple : compléter un arbre de probabilité
On donne les valeurs suivantes : \(P(A) = 1/3\), \(P_A(B)=5/7\) et \(P_\overline{A}(B)=3/5\).
On obtient :
\(P(\overline{A}) = 1 - 1/3 = 2/3\)
\(P_A(\overline{B})=1 - 5/7 = 2/7\)
\(P_\overline{A}(\overline{B})=1 - 3/5 = 2/5\)
Exemple : inverser un arbre de probabilité
\(P(B) = 1/3 \times 5/7 + 2/3 \times 3/5\)
\(P(B) = 5/21 + 6/15\)
\(P(B) = (25+42)/105 = 67/105\)
\(P(\overline{B}) = 1 - 67/105 = 38/105\)
\(P_B(A) = \dfrac{P(B \cap A)}{P(B)}\)
\(P_B(A) = \dfrac{5/21}{67/105}\)
\(P_B(A) = 5/21 \times 105/67 \)
\(P_B(A) = (5 \times 105) / (21 \times 67) \)
\(P_B(A) = 25/67 \) de là \(P_B(\overline{A}) = 42/67 \)
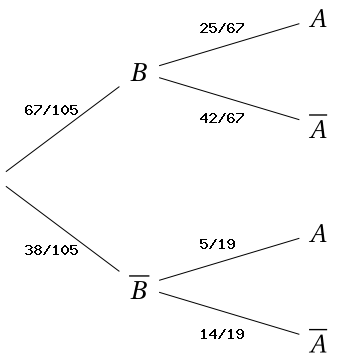
\(P_\overline{B}(A) = \dfrac{P(\overline{B} \cap A)}{P(\overline{B})}\)
\(P_\overline{B}(A) = \dfrac{2/21}{38/105}\)
\(P_\overline{B}(A) = 2/21 \times 105/38 \)
\(P_\overline{B}(A) = 5/19 \) de là \(P_\overline{B}(\overline{A}) = 14/19 \)

