Rechercher un outil (en entrant un mot clé):
Calculer la probabilité d'une Loi Binomiale
Une épreuve de Bernouilli désigne une expérience aléatoire indépendente qui possède 2 issues. On note généralement ces 2 issues : succé et échec, avec p la probabilité d'obtenir un succé à l'épreuve.
La probabilité d'obtenir un échec sera 1 – p on la note q.
La variable aléatoire X qui compte le nombre k de succès ou de réussite obtenus lorsque l'on répète une expérience de Bernouilli n fois suit la Loi Binomiale de formule :
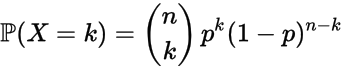
Propriétés :
Soit X une variable aléatoire suivant la loi binomiale de paramètres n et p.
- Son espérance est : E (X) = np
- Sa variance est : V (X) = np(1 − p)
- Son écart-type est : σ (X) = √[np (1 − p)]
L'outil calcule les valeurs de P( X ≤ a ) et P( a ≤ X ≤ b ) et la table de toutes les valeurs de P(X = k).
L'outil calcule l'intervalle [α,β] de fluctuation au seuil de 95%, tel que α est le plus petit entier tel que P(X ≤ α) > 0,025, et β est le plus petit entier tel que P(X ≤ β) ≥ 0,975.
Quelle est la probabilité d'obtenir 2 "six" en 5 lancés d'un dé cubique équilibré ?
L'épreuve de Bernouilli ici est : "obtenir "six" en lançant un dé cubique non truqué". Sa probalité p est égale à 1/6.
Le nombre d'essais est de 5. Le nombre de succés que l'on souhaite obtenir est 2.
La probabilité d'obtenir exactement 2 "six" est égale à :
P(X = 2) =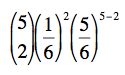 
= 0.16075
La probabilité d'obtenir au moins 2 "six" est égale à :
P(X ≥ 2) =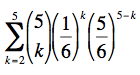 
= 0.19624
Intervalle de fluctuation au seuil de 95%
Un homme politique affirme que 52 % des électeurs lui font confiance. On interroge 100 électeurs au hasard (la population est suffisamment grande pour considérer qu'il s'agit de tirages avec remise) et on souhaite savoir à partir de quelles fréquences, au seuil de 95 %, on peut mettre en doute le pourcentage. On suppose la variable aléatoire X, correspondant au nombre d'électeurs lui faisant confiance dans un échantillon de 100 électeurs, suit la loi binomiale de paramètres n = 100 et p = 0.52.
Déterminer α et β tels que :
α est le plus petit entier tel que P(X ≤ α) > 0.025 et β est le plus petit entier tel que P(X ≤ β) ≥ 0.975.
L'outil nous donne l'intervalle [42,62]. p = 0.52 est élèment de l'intervalle [α/n,β/n] = [42/100,62/100] = [0.42,0.62]. L'affirmation de l'homme politique est donc acceptable au seuil de 95%.
