Calculis

Produit de matrices

Vous pouvez, grâce à cet outil, multiplier deux matrices en ligne afin d'obtenir leur matrice produit. Les matrices A et B peuvent même être de dimensions 4, 5 ou plus encore. Il est nécessaire, pour pouvoir faire le produit de deux matrices A et B, que le nombre de colonnes de la matrice A soit égal au nombre de lignes de la matrice B. Ainsi, les dimensions des matrices A et B doivent être respectivement (n,m) et (m,p). La matrice produit AB aura alors pour dimension (n,p) (voir les exemples de produits plus bas sur cette page).

Il suffit de rentrer chaque matrice de façon "naturelle" élément par élément, séparé d'un espace en effectuant un saut de ligne à chaque fin de ligne de la matrice. Vous pouvez entrer des entiers relatifs et des fractions de la forme -3/4 par exemple.

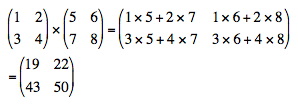
Exemple de produit de 2 matrices (2,3)×(3,2) :

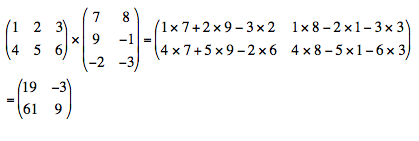
Exemple de produit d'une matrice carrée par son inverse :

 0  -7   0 -4 
 0   0   1  0 
 0 8/3   0 -2 
-5   0 6/5 -6 

24/185 6/25 63/185 -1/5 
 -3/37    0   6/37    0 
     0    1      0    0 
 -4/37    0 -21/74    0 

 1  0  0  0 
 0  1  0  0 
 0  0  1  0 
 0  0  0  1

Le résultat obtenu est la matrice identité, composée de 1 dans sa diagonale et de 0 pour les autres valeurs. Si on la note I, alors pour toute matrice carrée M de même dimension, on a : M × I = I × M = M et M × M^-1 = M^-1 × M = I .