Rechercher un outil (en entrant un mot clé):
Calculer l'équation d'une droite de régression linéaire
Cet outil détermine l'équation de la droite de régression linéaire (ou ajustement affine) d'une série statistique (ou nuage de points) de la forme (xi;yi). L'équation de la droite de régression linéaire est de la forme Y = aX + b avec :
a = ` {Cov(X,Y)} / {V(X)} ` et b = y − ax
où x et y sont les moyennes respectives des xi et yi. L'équation de la droite de régression est obtenue par la méthode des moindres carrés. Grâce à la droite de régression linéaire, il est possible de prévoir une tendance pour une valeur donnée X. De plus, l'outil calcule le coefficient de corrélation et les coordonnées du point moyen G(x ;y).
Remarque : on parle aussi d'interpolation linéaire à la place de régression linéaire.
* Dans le même ordre que les xi
** Pour laquelle vous souhaitez obtenir une tendance
Le coefficient de corrélation
Le coefficient de corrélation que l'on note r est égal à :
∑[ (xi − x)(yi − y) ] / √ [ ∑(xi − x)2 . ∑(yi − y)2 ]
Il varie entre −1 et 1. Plus sa valeur absolue est proche de 1, plus le modèle linéaire est fiable et décrit correctement la réalité.
Remarque : r et a sont de même signe.
Tendance d'une action
il s'agit de l'exemple par défaut de l'outil
Un particulier relève l'évolution de la valeur d'une action boursière au cours d'un mois. Il dispose de 1 000 titres de cette action.
| jour du mois | 2 | 7 | 13 | 15 | 20 | 24 | 25 | 29 | 30 | 31 |
| valeur en € | 3.62 | 3.78 | 4.32 | 4.14 | 4.88 | 5.01 | 4.94 | 5.39 | 5.28 | 5.42 |
1) Rechercher le point moyen de la série, c'est-à- dire la valeur moyenne de l'action du mois écoulé.
2) On souhaite ajuster le nuage de point. Déterminer l'équation de la droite de régression D qui passe par le point moyen. Est-ce que le système est bien linéaire ?
3) En supposant que la tendance sur le mois ecoulé se poursuive, estimer la valeur de l'action le 1er du mois suivant.
L'outil permet de répondre aux 3 questions precédante en rentrant les 2 séries suivantes :
xi : 2;7;13;15;20;24;25;29;30;31 et yi : 3.62; 3.78; 4.32; 4.14; 4.88; 5.01; 4.94; 5.39; 5.28; 5.42.
Pour calculer la tendance du 1er jour du mois suivant, il suffit d'entrer 32 pour 31+1.
Nous obtenons les résultats suivants :
Le point moyen a pour coordonnées (19.6 ; 4.678). La droite de régression linéaire admet pour équation Y = bX + a avec :
a = 0.065105680317041 et
b = 3.401928665786 .
Le coefficient de corrélationest r = 0.98. Le système est bien linéaire car r est proche de 1.
La valeur moyenne de l'action est donc de 4.678 €.
La prédiction pour la valeur 32 est égale à :
0.065105680317041×32 + 3.401928665786 = 5.4853104359313.
Ce particulier peut espérer pouvoir revendre l'ensemble de ses titres 5.48 € l'unité, le 1er jour du mois suivant.
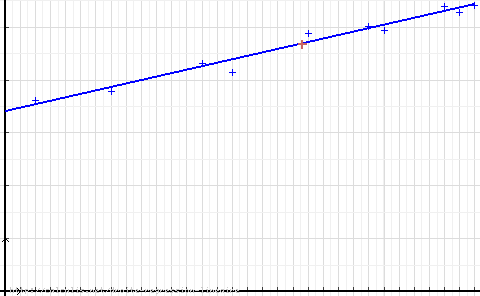
La droite de régression linéaire est proche de l'ensemble des points du nuage. Le système est bien linéaire. Le point moyen est représenté en rouge.

